Variance Inflection Factor
Table Of Contents:
- What Is VIF?
- How VIF Works?
- Mathematical Formula.
- Interpreting VIF Value.
- Example Of VIF.
- Why VIF Is Important?
- How To Handle High VIF?
- Summary.
(1) What Is VIF?
The Variance Inflation Factor (VIF) is a statistical measure used to detect multicollinearity in a regression model.
It quantifies how much the variance of a regression coefficient is inflated due to multicollinearity among the independent variables.
In simpler terms, VIF helps identify whether a predictor is strongly correlated with other predictors in the model.
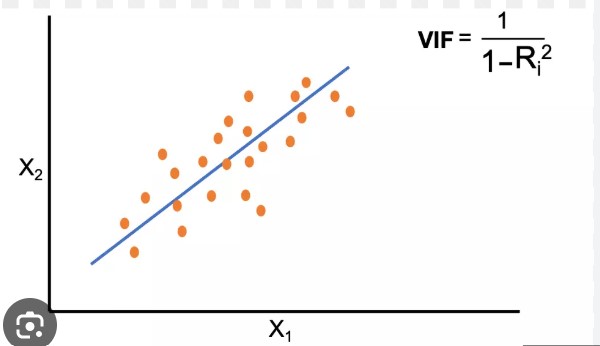
(2) How VIF Works?
- If an independent variable is highly correlated with other variables, the VIF for that variable will be high.
- A higher VIF means that the variable is contributing to multicollinearity, making the regression coefficients unreliable.
(3) Mathematical Formula.

(4) Interpreting VIF Value.

(5) Example Of VIF.

(6) Why VIF Is Important?
- Detecting Multicollinearity: High VIF values indicate strong multicollinearity, which can lead to unstable and unreliable regression coefficients.
- Guiding Variable Selection: By identifying variables with high VIFs, you can decide whether to remove or combine them to reduce multicollinearity.
(7) How To Handle High VIF.
- Drop Highly Correlated Variables: Remove one of the variables with high VIF, especially if it’s redundant or less important.
- Combine Variables: Combine correlated variables into a single variable (e.g., their average or principal components).
- Regularization: Use techniques like Ridge Regression or Lasso, which are less sensitive to multicollinearity.
- Centering: Transform variables by subtracting their mean (mean-centering) to reduce correlation.
(8)Why Does 𝑅 2 = 1 R 2 =1 Result in Maximum VIF?

(9) Summary
- The Variance Inflation Factor (VIF) is a valuable diagnostic tool to identify and mitigate multicollinearity in regression models, ensuring that the estimated coefficients remain stable and interpretable.

