Praudyog

Linear Regression – Assumption – 4 (Homoscedasticity In Details?)

admin

,

Homoscedasticity

Table Of Contents:

  1. What Is Homoscedasticity ?
  2. Why Is Homoscedasticity Important?
  3. How to Identify Homoscedasticity?
  4. Examples Of Homoscedasticity .
  5. Consequences of Violating Homoscedasticity.
  6. How to Fix Heteroscedasticity?
  7. In Summary.

(1) What Is Homoscedasticity?

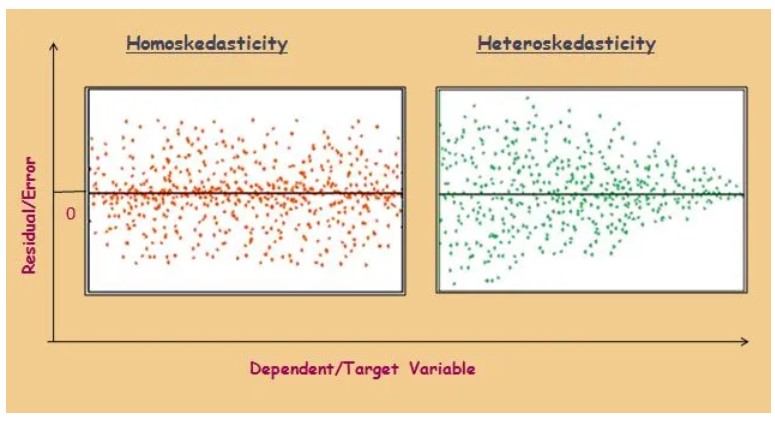
  • Homoscedasticity is an assumption in linear regression that the variance of the errors (residuals) is constant across all levels of the independent variables.
  • In other words, the spread of residuals should be roughly the same for all predicted values of the dependent variable.

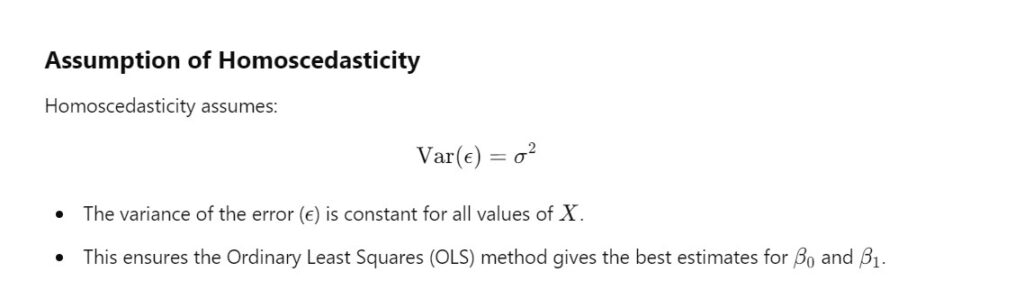
(2) Why Is Homoscedasticity Important?

Homoscedasticity is a key assumption in linear regression because:

  1. Accuracy of Predictions: When the variance of residuals is constant, the model’s predictions are more reliable.
  2. Valid Hypothesis Tests: Statistical tests like the t-test and F-test rely on the assumption of homoscedasticity for valid results.
  3. Minimized Bias: Violations of this assumption (heteroscedasticity) can lead to biased standard errors, affecting confidence intervals and hypothesis testing.

(3) How to Identify Homoscedasticity?

You can check for homoscedasticity by analyzing the residuals:

  1. Residual Plot:

    • Plot the residuals (errors) on the yy-axis against the predicted values (or independent variables) on the xx-axis.
    • Look for a random scatter of points without a clear pattern.
    • Homoscedasticity: Residuals have equal spread across all values.
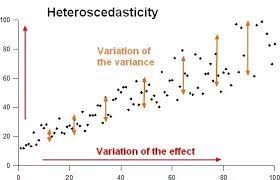
    • Heteroscedasticity: Residuals form a pattern (e.g., funnel shape, increasing or decreasing variance).

  2. Statistical Tests:

    • Breusch-Pagan Test: Tests if the residual variance depends on the predicted values.
    • White’s Test: A more general test for heteroscedasticity.

(4) Example Of Homoscedasticity.

Homoscedasticity:

  • Suppose you’re predicting house prices based on square footage. The variance of prediction errors is constant across small and large houses.

Heteroscedasticity:

  • Predicting income based on age: Younger individuals might have a smaller spread of incomes (e.g., low-paying entry-level jobs), while older individuals could have a wider spread (e.g., executive positions vs. retirees).

Example-1:

Example-2:

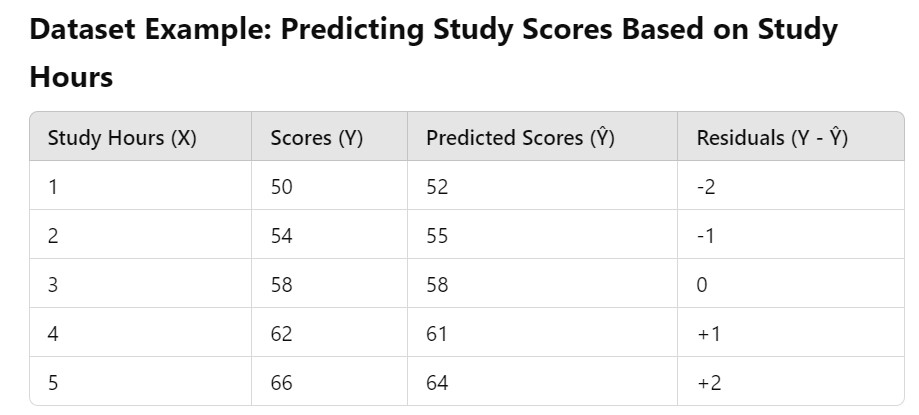
Example-3:

import matplotlib.pyplot as plt
import numpy as np

# Generate data for Homoscedasticity
np.random.seed(0)
x_homo = np.linspace(1, 10, 50)
y_homo = np.random.normal(0, 1, size=50)

# Generate data for Heteroscedasticity
x_hetero = np.linspace(1, 10, 50)
y_hetero = np.random.normal(0, x_hetero / 2, size=50)  # Variance increases with x

# Plot Homoscedasticity
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.scatter(x_homo, y_homo, color='blue', alpha=0.7, label='Residuals')
plt.axhline(y=0, color='black', linestyle='--', linewidth=1)
plt.title("Homoscedasticity: Constant Variance")
plt.xlabel("Predicted Values")
plt.ylabel("Residuals")
plt.legend()

# Plot Heteroscedasticity
plt.subplot(1, 2, 2)
plt.scatter(x_hetero, y_hetero, color='red', alpha=0.7, label='Residuals')
plt.axhline(y=0, color='black', linestyle='--', linewidth=1)
plt.title("Heteroscedasticity: Increasing Variance")
plt.xlabel("Predicted Values")
plt.ylabel("Residuals")
plt.legend()

plt.tight_layout()
plt.show()

(5) Types of Datasets Likely to Have Heteroscedasticity

1. Financial Data

  • Example: Predicting stock prices based on market indicators.
  • Reason:
    • Larger companies or high-priced stocks may show higher variability in returns compared to smaller companies or lower-priced stocks.
    • Variance increases as stock prices or market values increase.

2. Income vs. Expenditure

  • Example: Predicting monthly expenditures based on income levels.
  • Reason:
    • Individuals with higher incomes tend to have more variable spending habits compared to those with lower incomes.
    • Variance of expenditure grows as income increases.

3. Housing Prices

  • Example: Predicting house prices based on square footage or number of bedrooms.
  • Reason:
    • Larger, more expensive houses often have greater variability in price due to factors like luxury features, location, and market conditions.
    • Variance in price increases with house size or features.

4. Education Data

  • Example: Predicting student test scores based on study hours.
  • Reason:
    • For students who study less, the variability in scores might be low (most will score poorly).
    • For students who study more, scores can vary widely based on other factors like aptitude and preparation.

5. Retail Sales Data

  • Example: Predicting sales revenue based on the number of customers or advertisement spending.
  • Reason:
    • Higher levels of advertising or larger customer bases might lead to more variable sales outcomes due to external factors (seasonality, competition).

6. Health Data

  • Example: Predicting healthcare costs based on age or BMI.
  • Reason:
    • Younger individuals typically have lower and more consistent healthcare costs.
    • Older individuals or those with higher BMI may have highly variable costs due to chronic conditions or treatments.

7. Insurance Claims

  • Example: Predicting insurance claim amounts based on the value of insured assets.
  • Reason:
    • High-value assets (e.g., luxury cars, expensive properties) often have more variable claims compared to lower-value assets.

8. Demographic and Survey Data

  • Example: Predicting happiness scores based on income or age.
  • Reason:
    • Variability in happiness might be low at extreme poverty levels but increases significantly at higher income levels due to diverse lifestyle choices.

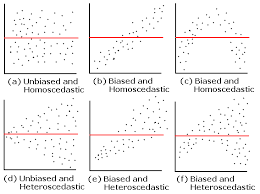
(5) Consequences of Violating Homoscedasticity

When homoscedasticity is violated (heteroscedasticity occurs):

  1. Biased Standard Errors:
    • Standard errors of the coefficients are incorrect, leading to unreliable t-tests and confidence intervals.
  2. Invalid Hypothesis Tests:
    • P-values for coefficients might be misleading, making it harder to assess their significance.
  3. Reduced Model Efficiency:
    • Ordinary Least Squares (OLS) estimators are no longer the Best Linear Unbiased Estimators (BLUE).

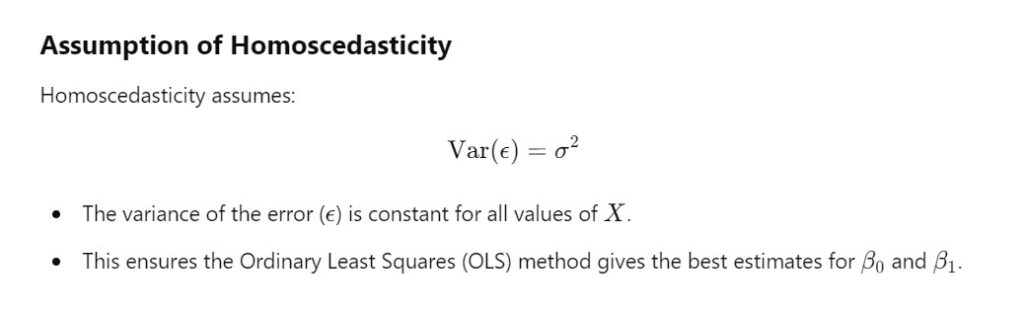
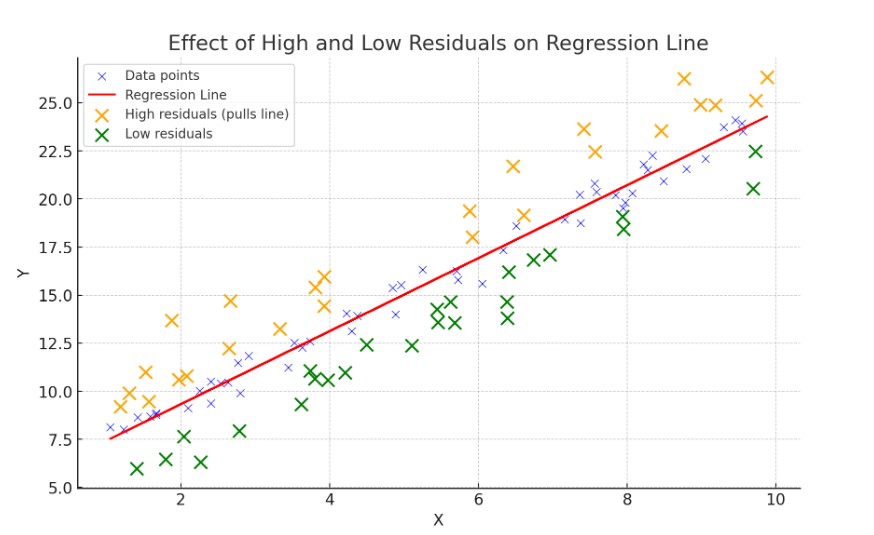
How Change In Variance Cases Inefficient In Beta?

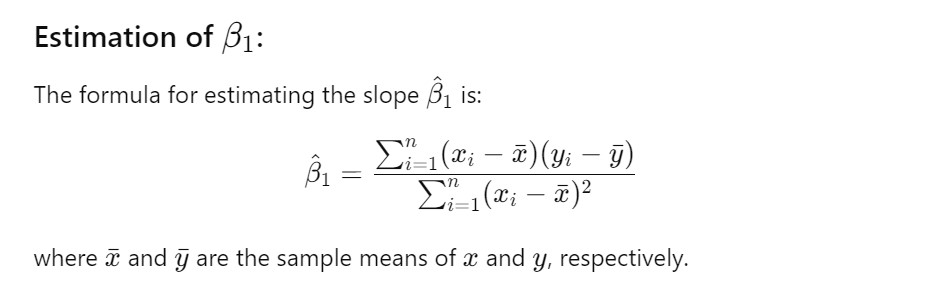
Example

(7) How Biases Standard Error Occur ?

(8) How to Fix Heteroscedasticity?

(9) Summary

  • Homoscedasticity: Equal spread of residuals across all predicted values.
  • Key Assumption: Ensures accurate predictions and valid statistical inference.
  • Check: Residual plots and statistical tests.
  • Fix: Transformations, weighted regression, or robust methods.

Leave a Reply

Your email address will not be published. Required fields are marked *