Why We Don’t Use Gradient Descent Algorithm In Linear Regression?
Table Of Contents:
- hI
(1) Reason
- We do apply gradient descent to linear regression, but often it’s not necessary because linear regression has a closed-form solution that is computationally efficient for small to medium-sized datasets.
- Let me explain:
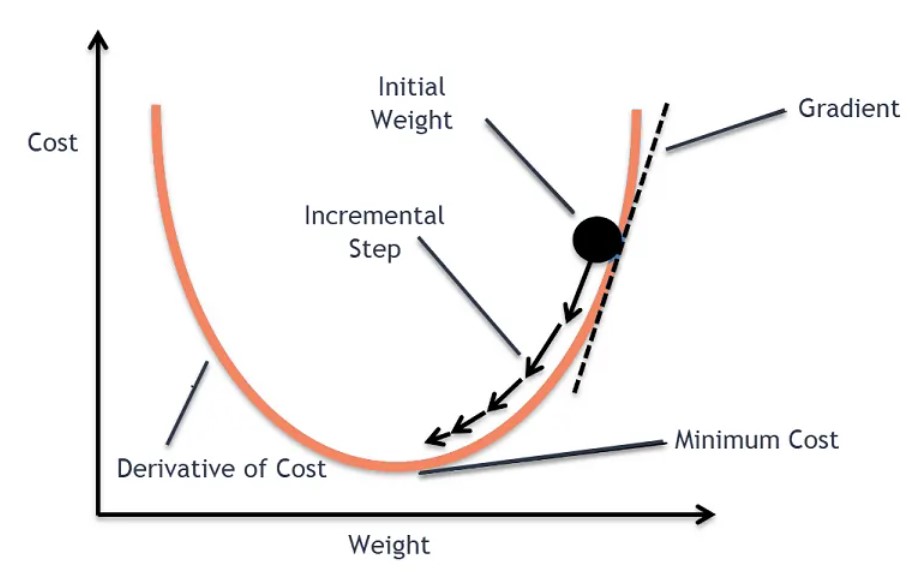
Closed-Form Solution for Linear Regression




- Here we can directly take the derivative of the Loss function and equate it to zero.
- Then we can solve the equation to get the optimal value of the beta.
How Can We Directly Equate A Single Derivative To Zero To Get The Beta Value.
- We can directly use the single derivative to zero because of simple nature of the loss function.
- Yes, for quadratic loss functions (like the Mean Squared Error (MSE) in linear regression), it is mathematically feasible to equate the loss function’s derivative to zero and solve for the parameters analytically.
- However, directly equating the loss function itself to zero is generally not practical in most cases. Let’s understand why: