Transformers – Positional Encoding
Table Of Contents:
- What Is Positional Encoding In Transformers?
- Why Do We Need Positional Encoding?
- How Does Positional Encoding Works?
- Positional Encoding In Attention All You Need Paper.
- Interesting Observations In Sin & Cosine Curve.
- How Positional Encoding Captures The Relative Position Of The Words ?
(1) What Is Positional Encoding In Transformer?
- Positional Encoding is a technique used in Transformers to add order (position) information to input sequences.
- Since Transformers do not have built-in sequence awareness (unlike RNNs), they use positional encodings to help the model understand the order of words in a sentence.
(2) Why Do We Need Positional Encoding In Transformer?

(3) How Does Positional Encoding Works?
Step – 1: Benefits Of Self Attention Mechanism
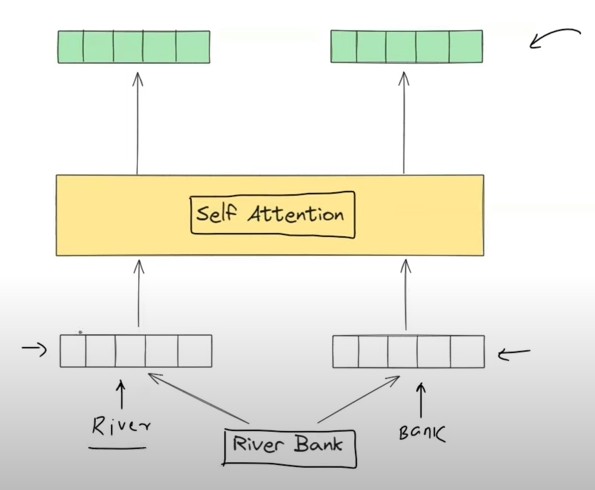
- We have already understood that how does the self attention block works.
- You pass the static embedding of the word and it will give you the contextual embeddings of that particular word.
- For example, Sentence-1: “River Bank” and Sentence-2: “Money Bank”, for the word ‘Bank’ the contextual embedding will be different in both of the sentence.
- This was the best part of the self attention mechanism.
- Another benefit of the contextual embedding is that you can parallelly get the contextual embedding of every word if you have GPU support.
- You can pass the entire sentence at a time and can get the contextual embedding of every word.
- This makes the Self Attention super faster.
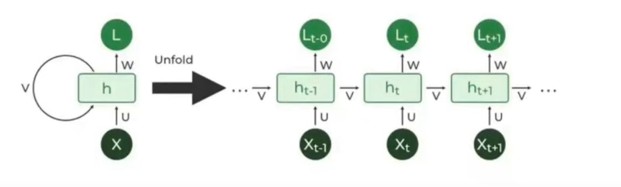
- You can compare this with RNN in this case you have to process each words one after another.
- This takes lot of time to process the huge sentences.
- This drawback has been solved in the Self Attention mechanism.
Step – 2: Drawbacks Of Self Attention Mechanism
- The major drawbacks of Self Attention mechanism is that it cant capture the order of the words in a sentence.
- Sentence -1: I love Arpita.
- Sentence-2: Arpita Loves Me.
- The Self Attention mechanism both the sentences are same. Because it processes the words parallelly.
- This problem does not exists in RNN mechanism.
Step – 3: Need Of Positional Encoding.
- This is where Positional Encoding comes into play.
- Positional Encoding encodes the position of the words in the sentence.
Step – 4: Understanding Positional Encoding.
Solution-1: Add Positional Numbers
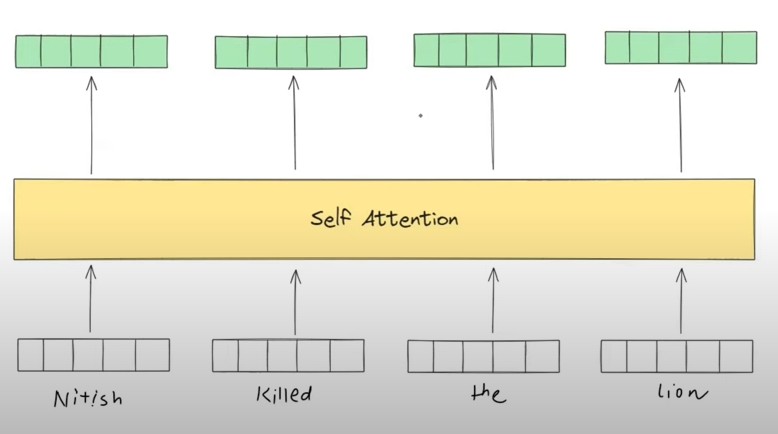
- We have 4 words in a sentence, ”Nitish Killed The Lion”, but the problem is our Self Attention mechanism does not understand which word come 1st 2nd 3rd and 4th.
- Somehow I need to pass the order of the words to my Self Attention model.
- The simple solution will be , i will assign the numbers in order based on there occurrence.
- Suppose the word embedding is 512 dimension what I will do is that I will add one more dimension to it which will store the position of the word.
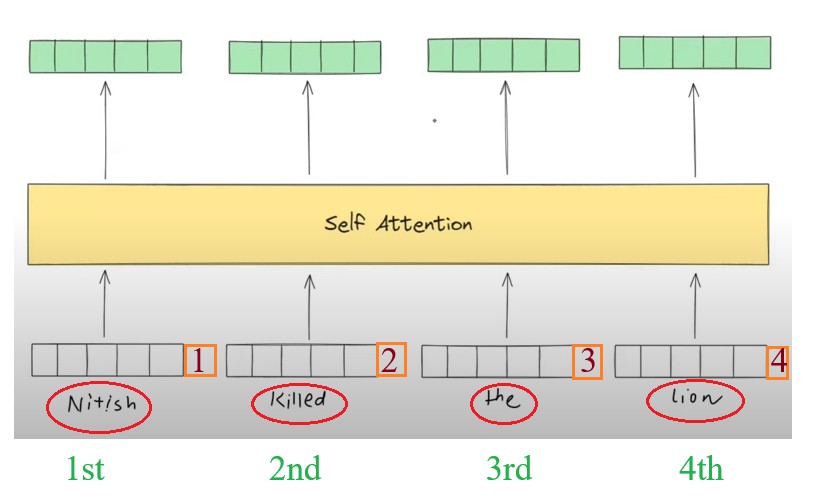
- Now my current dimension will be 512 +1 = 513 Dimension.
Solution-1: Problems
- Unbounded Issue :
- This approach is unbounded, means there is no upper limit to this approach.
- Suppose you have millions of word then you last word will have 10,00000/- as the positional value.
- As the Transformation model works on ANN approach and it uses backpropagation to update the weights.
- And backpropagation hates big numbers it can cause exploding gradient issue with the weights with this big number.
- It will create instability in training process.
- The solution you can propose is that you can normalize the numbers between 0 to 1.
- What you can do is that you can divide each numbers with the total number and it will become in the range 0 to 1.
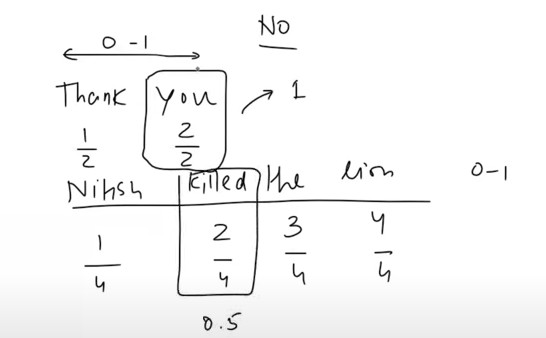
- Suppose you have two sentences,
- Sentence-1: – “Thank You”
- Sentence-2: – “Nitish Killed The Lion”
- Once you do the normalization you will get the position values like this displayed in the above image.
- In the 1st sentence the position of 2nd word “You” will be 1 and in the 2nd sentence the position of the 2nd word “Killed” is 0.5.
- Both the words are in second position but if we are using normalization the 2nd position value sometimes is 1 and also it is 0.5.
- Your model will confuse what actually is the 2nd position value , is it 1 or 0.5 ?
2. Discrete Number Issue :
- 1,2 3,4 5 .. are the discrete numbers and these are not good for neural networks.
- Neural networks generally prefers smooth transactions like contentious numbers.
- Discrete number will cause the gradient instability.
3. Does not Captures The Relative Position:
- With this approach you can’t capture the relative position of the numbers.

- These positions are called the absolute position. But it cant say the relative position of the words.
- Relative position means 3rd word is how many distance away from the 1st word.
- We can’t calculate the distance between two words.
- Because our neural network cant able to figure out the in between numbers, between the two absolute value.
- Neural network model should know how the numbers transitioned from 1 to 2 then only it can find out the relative position of the words.
- It will be better if we have the periodic function to represent the position of the words.
- For example: the difference between positions 5 and 6 will have a similar pattern to 10 and 11.
- This is useful for translation, generation, and other sequence tasks where relative position matters.
Super Note:
- The question is why can’t we get the relative position of the words by using the absolute number?
- Answer to this question is , if you have two positions like 5 and 8, you can say position 5 is 3 distance away from position 8, but the catch here is your model doesn’t know how to calculate this difference 8 – 5 = 3.
- But if we use the Sin or Cosine curve by seeing the pattern in the curve like position 5 and 6 is similar distance like position 8 and 9. By seeing the pattern of the curve our model will learn the relative position of the words in a sentence.
Conclusion:
- Hence we want a Bounded, Continuous and Periodic function to represent the position of the words in a sentence.
- One such functions will be the trigonometric functions.
- Like Sin(x), Cos(x) etc.
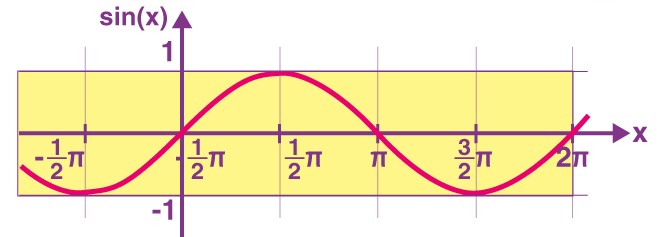
- A “Sin(x)” Function ranges from -1 to 1.
- The ‘Sin(x)’ function is continuous always.
- The ‘Sin(x)’ function is also periodic in nature.
Step – 5: Using Sin Function As Positional Encoding
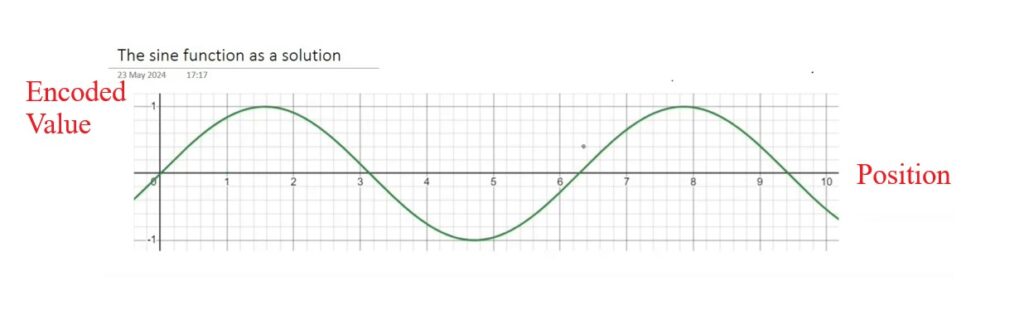
- X – axis represents the position of the words.
- Y- axis represents the positional encoding values of the corresponding word.


- Now you will add positional encoding value at the end of the embedding like in the below image.
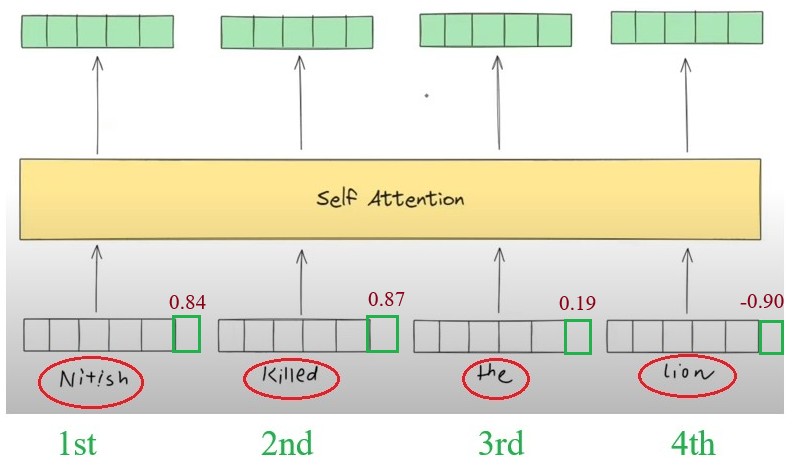
- The best part of this approach is that it solves 3 problems of the previous approach.
- It is bounded , continuous and periodic in nature.
Problem With Sin Curve Encoding:
- Itis mandatory to have the unique positional encoding value for each word.
- But if we are using a periodic function its value repeats in the next cycle.
- Hence there is chances that two words will have same positional encoding value which will be wrong.
- Periodicity is helping in the same time it has also some disadvantages.
Solution To The Problem With Sin Curve Encoding:
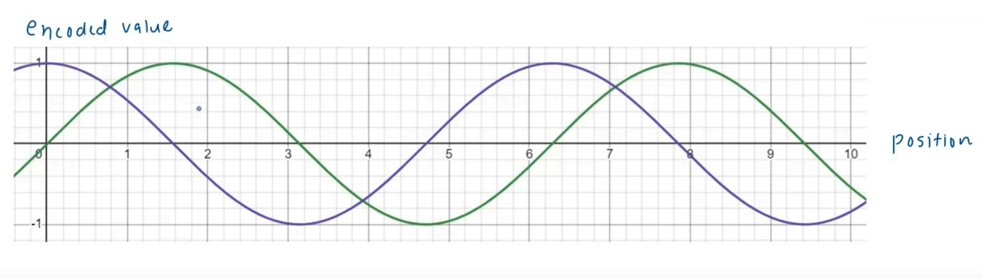
- The solution to this problem will be instead of using one mathematical function we can use 2 mathematical functions.
- We can use Y = Sin(Position) and Y = Cos(Position).
- What will happen now is , for every word we will have 2 positional encoding values.
- One value will be from Sin Function and another value will be from Cosine function.
- Now for every word instead of representing it as a scalar you can represent it as a vector as a set of numbers.
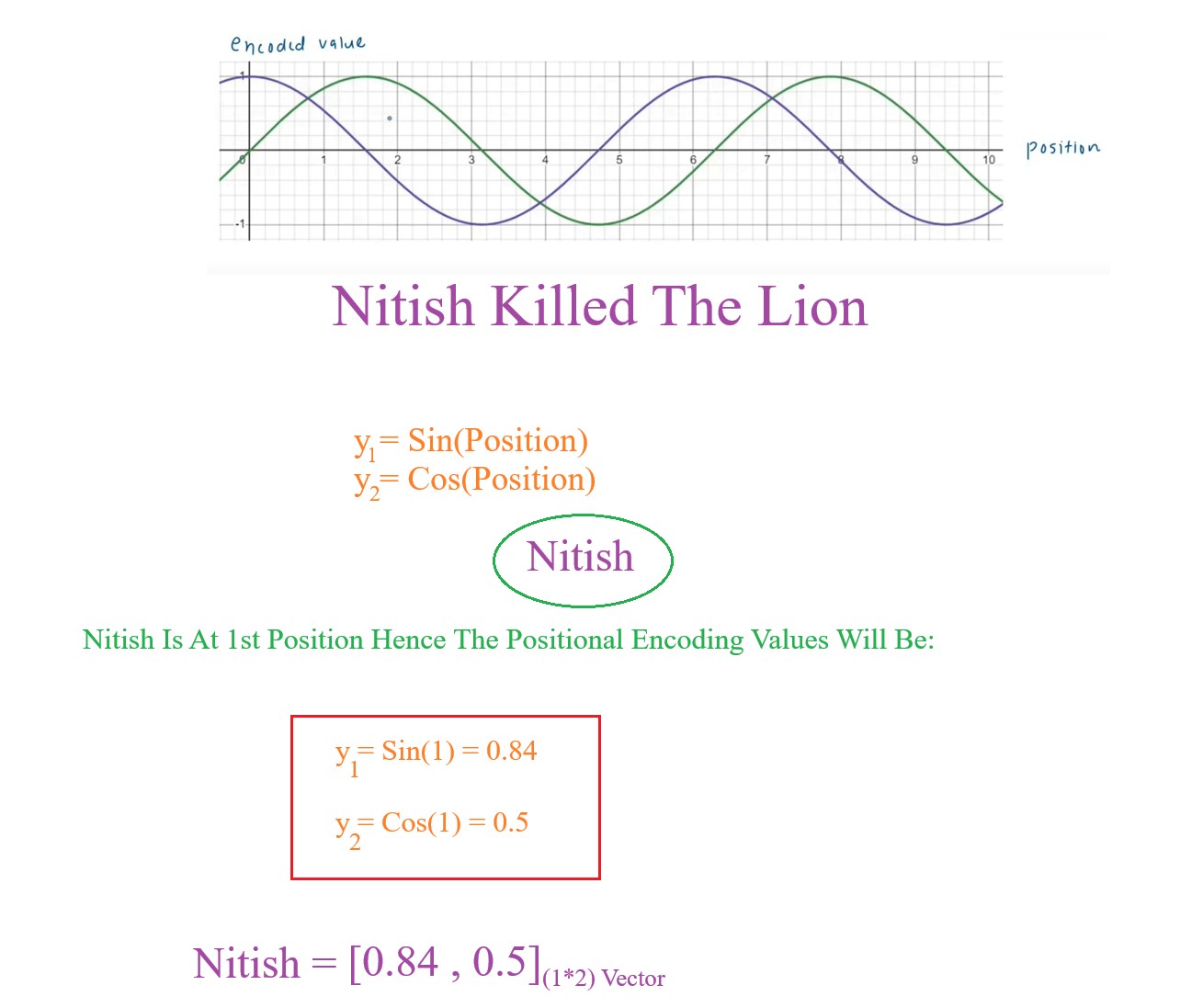
- From the above diagram we can see that for the word Nitish we got 2 positional encoding values 0.84 and 0.5.
- And we can represent it as a vector as [0.84 , 0.5]
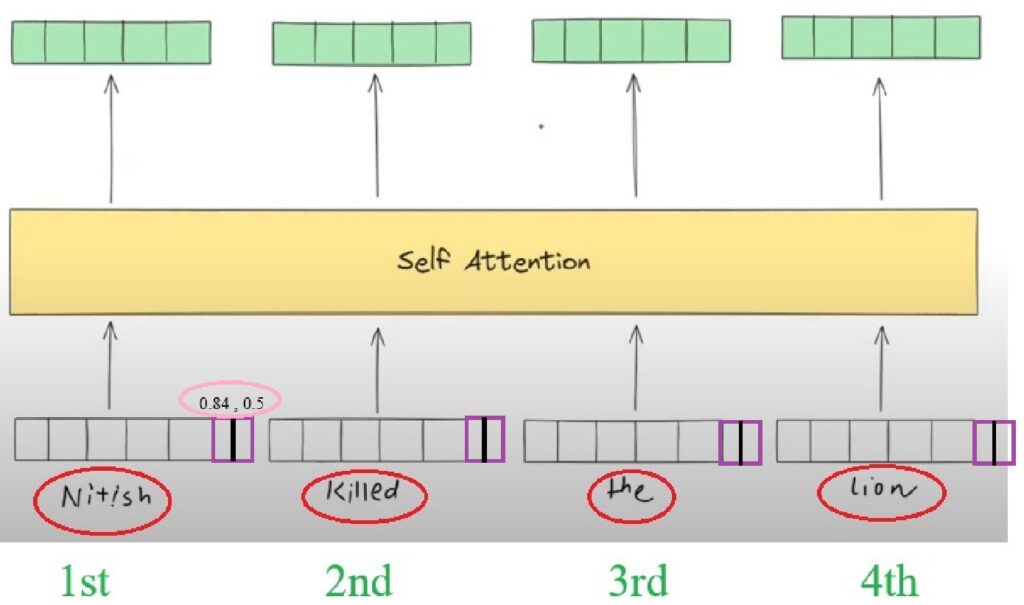
- Hence instead of adding one positional value we need to add two positional values.
- In the above diagram i have added 0.84 and 0.5 as positional encoding values.
- Similarly we can find out the positional encoding value for the word “Kills”, here the position value will be 2.
- We need to find out Sin(2) and Cos(2).
How Adding 2 Periodic Function Solves The Problem Of Similar Positional Encoding Value?
- If we are using a single scalar value as the positional encoding value there is a high chance that we will get a similar scalar value for other words.
- If we are using 2 positional encoding value there is quite less chance that two numbers will be same.
- Hence we have reduced the risk of similar positional encoding value for two words.
- In real life we can use more than 2 positional encoding value also.
- There is a high chance that we will get same positional encoding value for two words.
- Hence what we can do is to increase the number of Sin and Cosine curves to generate the more number of positional encoding value.
- Like in the below image we have 2 Sin and 2 Cosine curves.
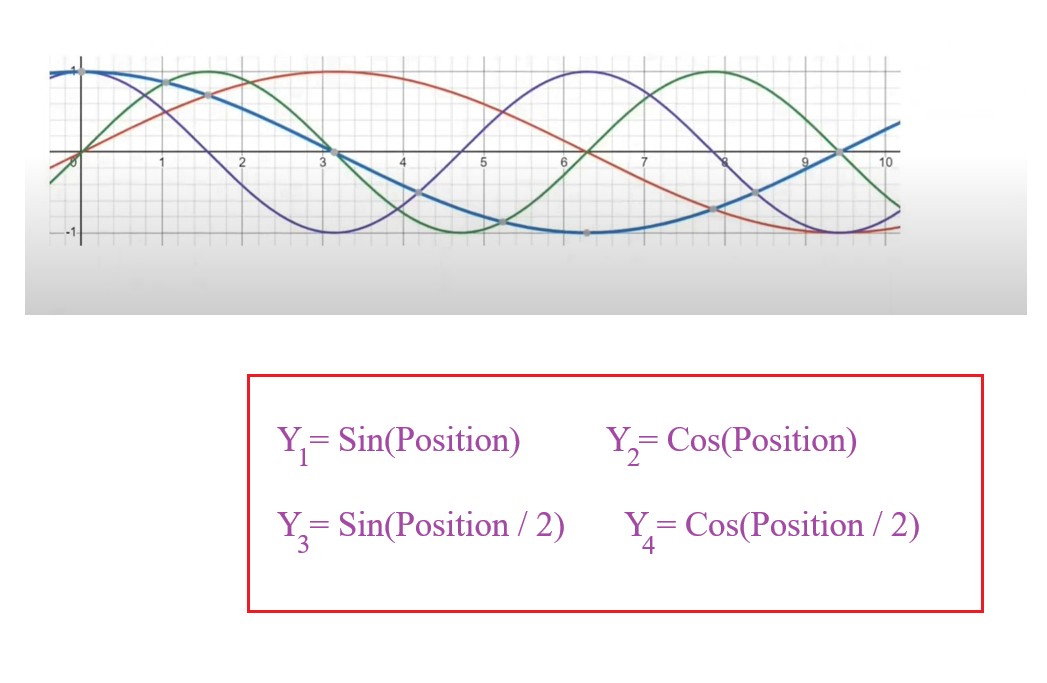
- Now calculate the positional embedding of the word “Nitish”.

- With this 4 positional encoding value we have reduced the probability of getting same positional encoding value.
- You can also increase the Sin and Cos function by doing Sin(Position/3) and Cos(Position/3).
(4) Positional Encoding In Attention All You Need Paper.
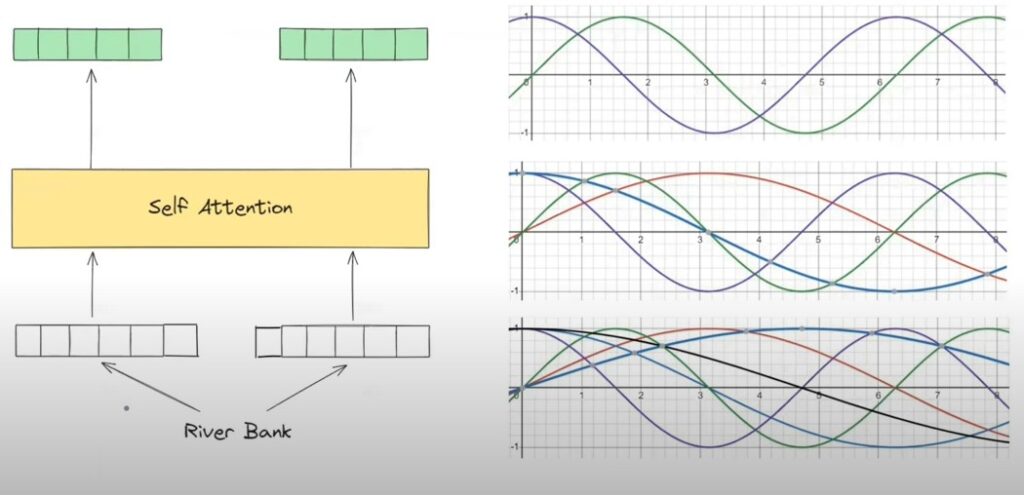
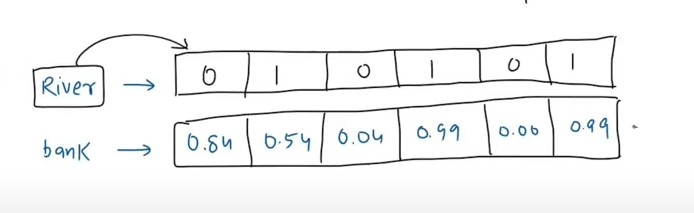
- Consider we have one sentence “River Bank”. We need to calculate the positional encoding for both of the words before passing it into the self attention model.
- I will use the multiple Sin and Cosine curves to calculate the positional encoding of the word.
- Question: The question now is what will be the dimension of the positional encoding vector?
- Answer : The dimension of the positional encoding vector for the word “River” will be same as its embedding vector.
- If river word having 6 dimension embedding vector then the dimension of the positional encoding vector will also be 6.
- Question: How to use the positional encoding vector with the embedding vector ?
- Answer: In Attention All You Need paper what they are doing is they are adding the two vectors together instead of concatenating them together.

- Now this vector will have both the information.
- One is Embedding information and another is positional encoding vector information.
- Question: What Was The Problem With Concatenation?
- Answer: If you are concatenating 6 dim with another 6 dim vector it will be 12 dimension vector which is huge.
- It will increase the dimension of the original vector.
- It will cause the increase in number of parameters in the neural network model .
- Interns it will increase the training timing of the model.
- Hence we are making addition of two vectors.
- Question: How to calculate the values of the positional encoding vector?
- Answer: You will use Sin and Cosine functions to calculate the positional encoding values.
- If you have 6 dimension you will use(Sin, Cosine, Sin, Cosine, Sin , Cosine) like this combination.
- Now lets find out the positional encoding vector for the word ‘River’.
- Here the position of the word ‘River’ = 1.
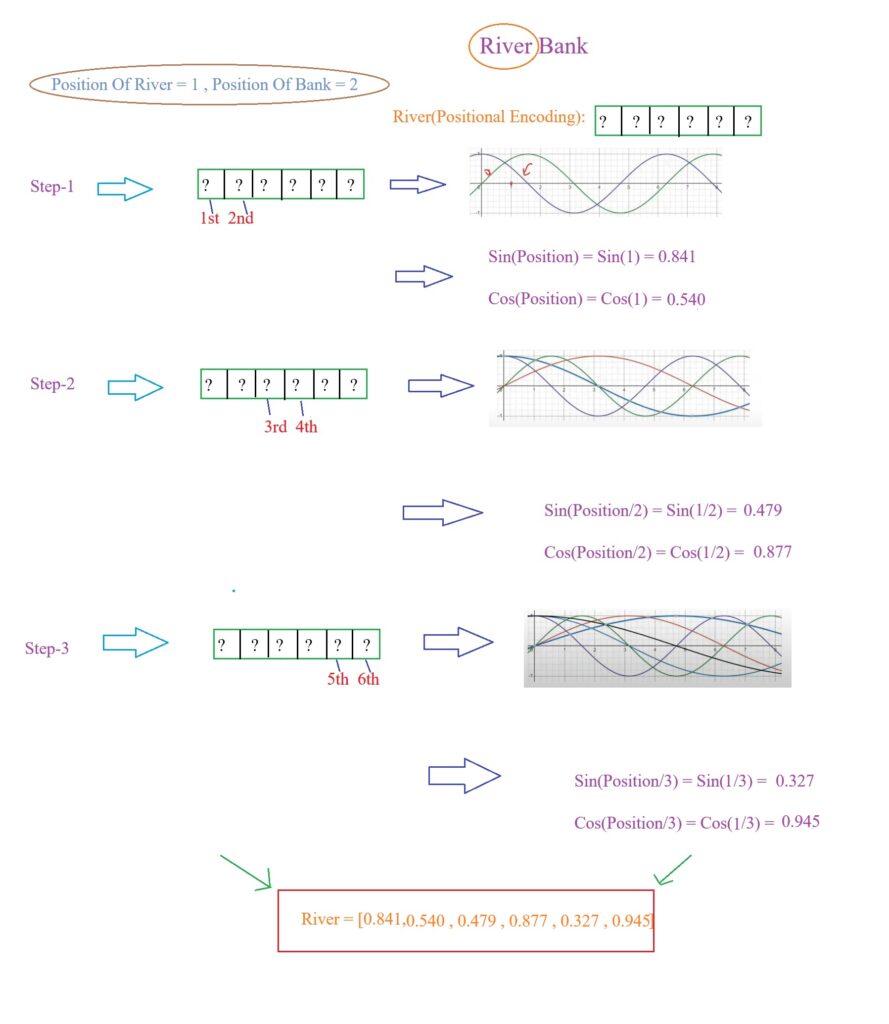
- For the word ‘Bank’ we will use Position = 2 and will calculate the 6 dimensional positional encoding value.
- In the research paper they have used 512 word embedding vector hence we have to use 512 positional embedding vector.
- To generate 512 positional embedding vector we have to use 64 pairs of Sin and Cosine functions(64*2 = 512 Dimension).
Key Points To Note:
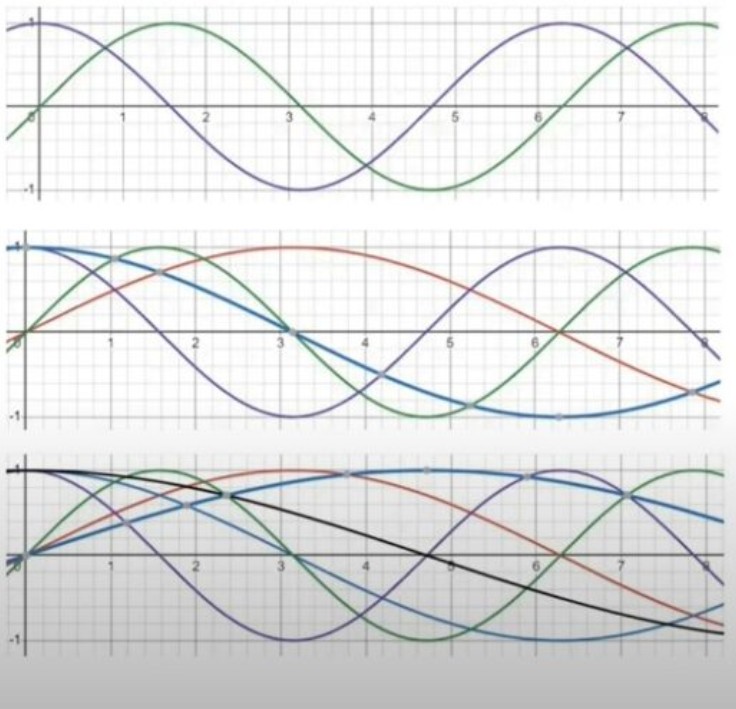
- One thing you can notice is that as the number of dimension increases the frequency of the curve is decreasing.
- Question: How Do You Decide The Frequency Of The Curves?
- Answer: We will use below formula to find out the positional Encoding of the words.
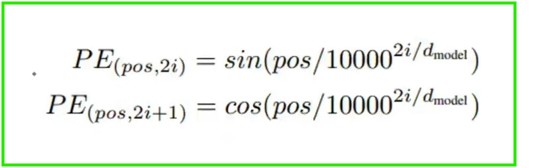
- Let us calculate the positional encoding of the word River in the sentence “River Bank”.

- Similarly we will calculate the positional encoding of the word Bank in the sentence “River Bank”.
- Here pos = 1
(5) Interesting Observations In Sin & Cosine Curve.

- Why the frequency of the sin and cosine curve reduces as the dimension increases.
- We will get the answer from the below heatmap diagram.
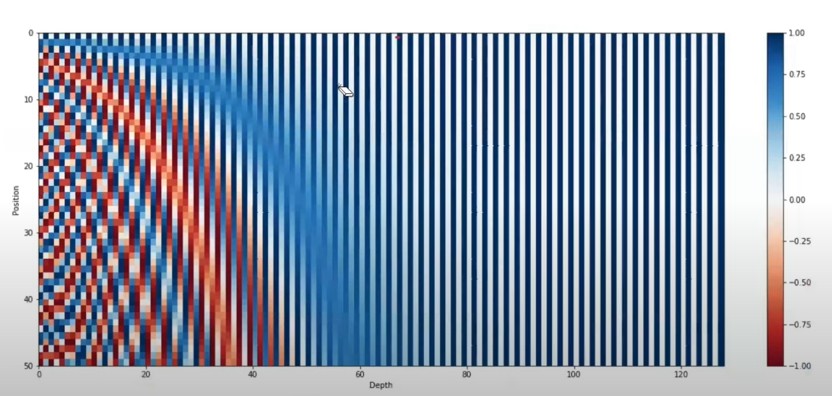
- Suppose we have 50 words sentence and the embedding of each words in the sentence = 128 bit.
- dmodel = 128.
- For 50 words how many positional encoding vectors you have to calculate?
- Answer = 50.
- Dimension of each positional encoding vector = 128.
- In the above graph the X-axis represents the positional encoding values from 0 to 128.
- In the Y-axis we have 50 number of words.
- for the first word we can see that the color is changing in between white , black till the end.
- Which means the positional embedding of the first word is [0 1 0 1 0 1 …… till 128].
- From the above heat map diagram you can see that most of the differences in the positional encoding vectors you can see in lower dimensions.
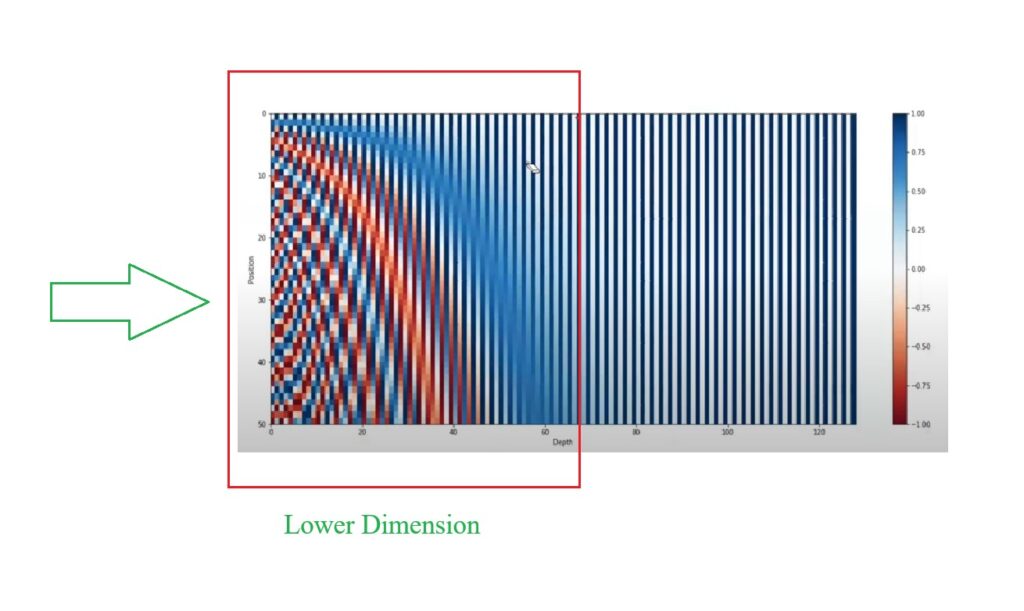
- You can see that there is no change in the embedding values in the higher dimension.
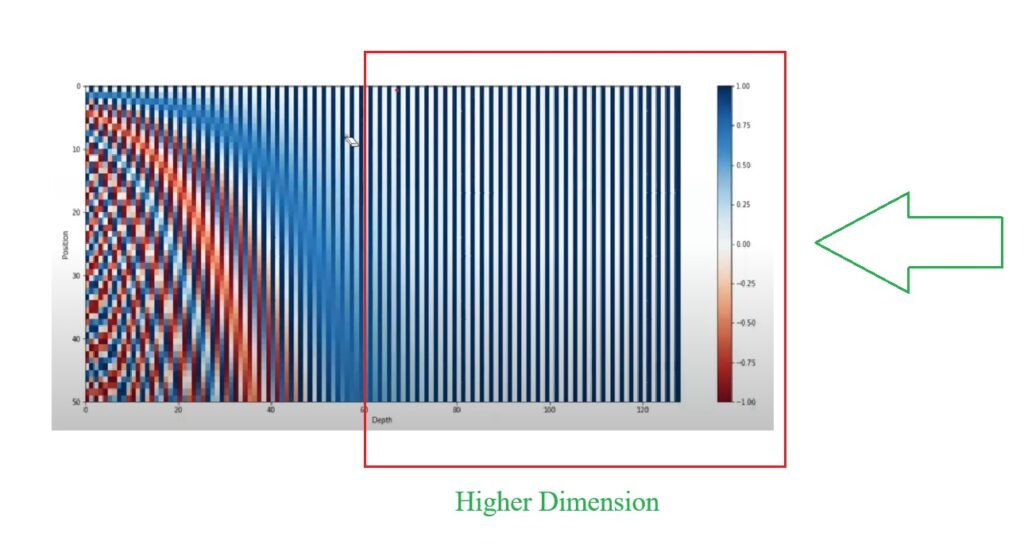
- For higher dimension it is not changing because, you have taken low frequency sin and cos curves.
- For lower dimensions you have taken higher frequency curves which is changing quite fast.
- This you can see in the image below.

- If your word count increases from 50 to 100 your higher dimension values will also get change.
- Because, your X axis represents the position of the words in the sentence, if your x axis length increases your sin and cosine curve will have more space to complete its cycle and you will see changes in higher dimension of positional encoding values.
(6) How Positional Encoding Captures The Relative Position Of The Words ?

- The above graph represents the heatmap of the positional encoding values for 50words in 128 Dimension.
- The X – axis represents the dimensions of the positional encoding values. Each word will have 128 dimension.
- The Y – axis represents the position of the words from 1 to 50.
Key Observations:
- The way we have applied the Sin and Cosine approach to solve the positional encoding problem, it inherently added one benefit to my model.
- Let us plot 50 vectors in the graph .
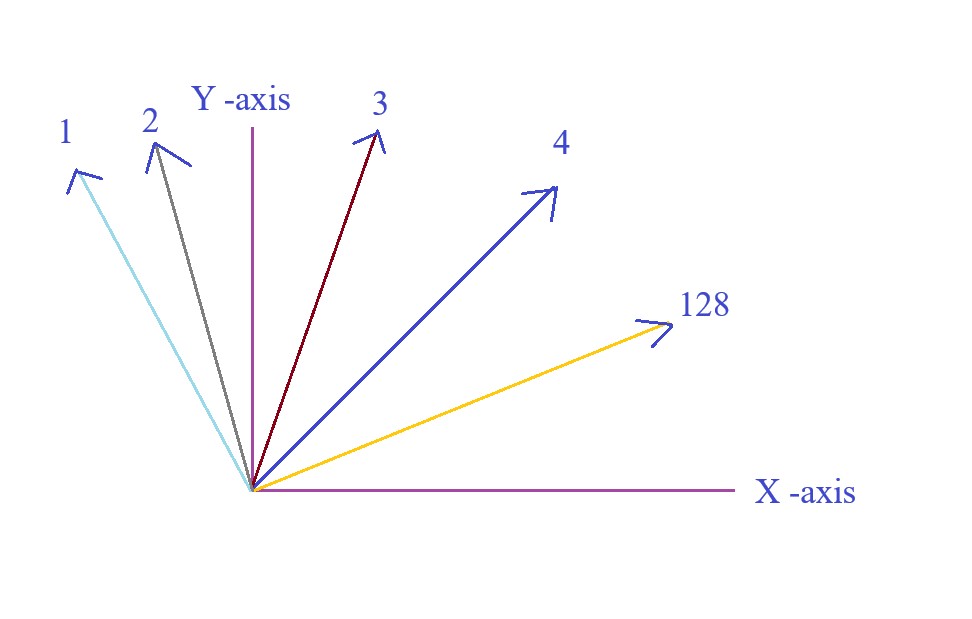
- Suppose I pickup one particular vector, vector No – 10.
- If I will apply one linear transformation on the vector number 10, means i will multiply it with a matrix.
- For a particular matrix we will see that, if we apply that matrix on V10 i will automatically get V20.
- This is displayed in the below image.
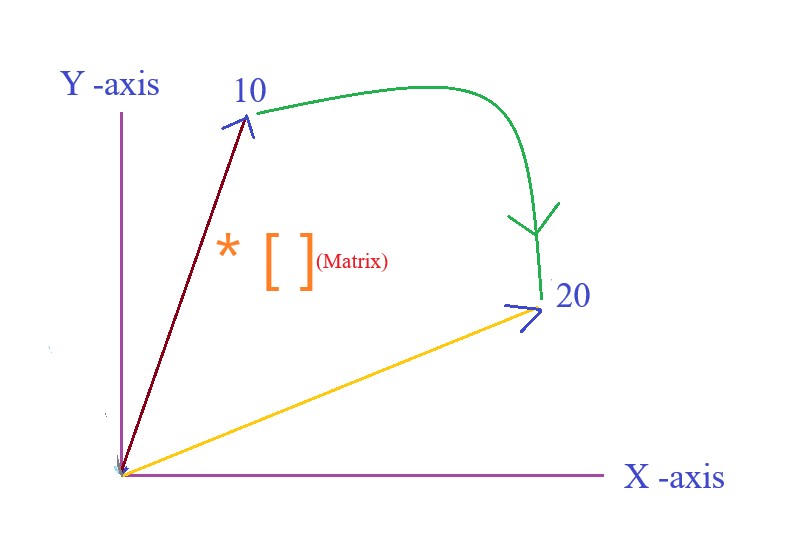
- If I will apply the same matrix on V30, I will move to V40.
- If I will apply the same matrix on V40, I will move to V50.
- So in a way the interesting property here is that the particular matrix is having the capability of moving a distance of 10 Delta.
- One more interesting thing is this , suppose we are at V5 and we apply the matrix on it and it gives us V10, what if i take the same matrix and apply it on V12 I will move to V17. Which means the 2nd matrix is having the capability of covering a distance of 5 delta.
- The main concept here is for each delta/distance we have one matrix available by taking help of that matrix we can move from any place to any other place.
- By this way this positional encoding is having the capability of understanding the positional encoding of the words.
- Now the main question will be how the Matrix will looks like ? You can go through this blog to understand how this matrix looks like.
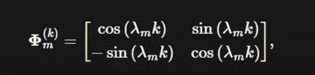
- The above matrix is having the sin and cosine components on it.
- Why we took sin and cosine components in positional encoding we would have taken only sin component.
- Because we have used both the sin and cosine component due to this the math is converging in a way that you are able to capture the relative position of the words in a sentence.
https://blog.timodenk.com/linear-relationships-in-the-transformers-positional-encoding/
