-

Accuracy, Precision, Recall, F1-Score
Confusion Metrics, Accuracy, Precision, Recall, F1-Score Table Of Contents: Confusion Metrics Accuracy Precision Recall F1-Score Specificity (True Negative Rate) Fall-Out : False Positive Rate (FPR) Miss Rate: False Negative Rate (FNR) Balanced Accuracy Example Of Confusion Metrics Confusion Metrics For Multiple Class (1) Confusion Metrics A confusion matrix is a tabular representation of the performance of a classification model. It helps visualize and understand how well a model’s predictions align with the actual outcomes, especially in binary and multi-class classification. (2) Structure Of Confusion Metrics Definition: (3) Accuracy For imbalanced dataset Accuracy will give the wrong impression about the model
-
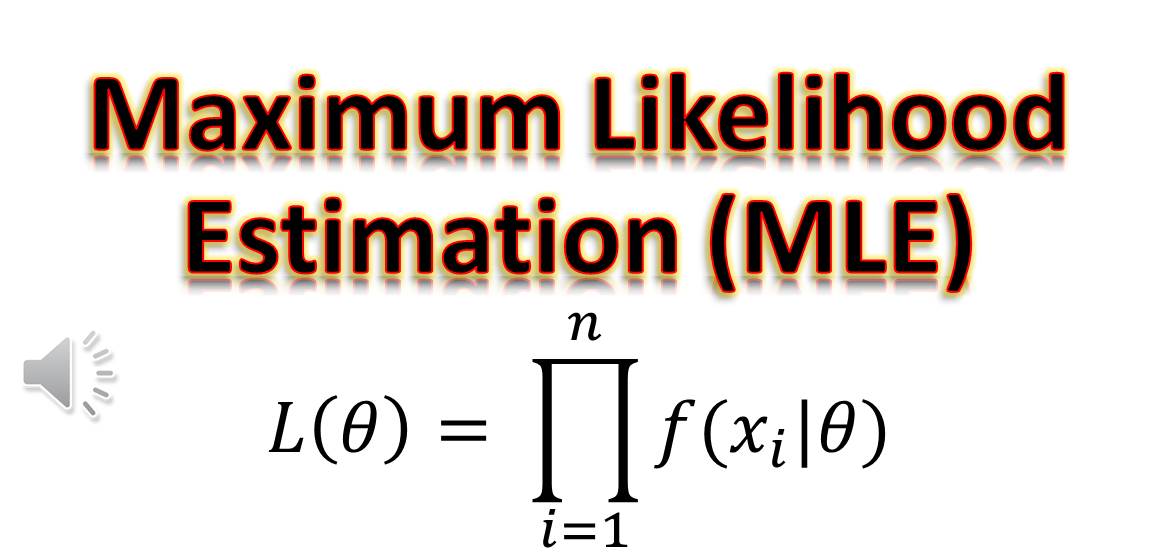
Why We Use Maximum Likelihood Estimation In Logistic Regression?
Why We Use Maximum Likelihood Estimation In Logistic Regression? Maximum Likelihood find out where the Probability is maximum. Minimizing the Loss identifies where the loss is minimum. Table Of Contents: Difference In Maximizing Likelihood and Minimum Loss. (1) How To Find Maximum Likelihood? (2) Maximum Likelihood For Logistic Regression (3) Difference In Maximizing Likelihood and Minimum Loss. (2) Why Differentiating To Zero Gives Us Maximize Log-Likelihood: Differentiating a function and setting it equal to zero helps us find the critical points, which could be maxima, minima, or saddle points. In the context of Maximum Likelihood Estimation (MLE), this principle is
-
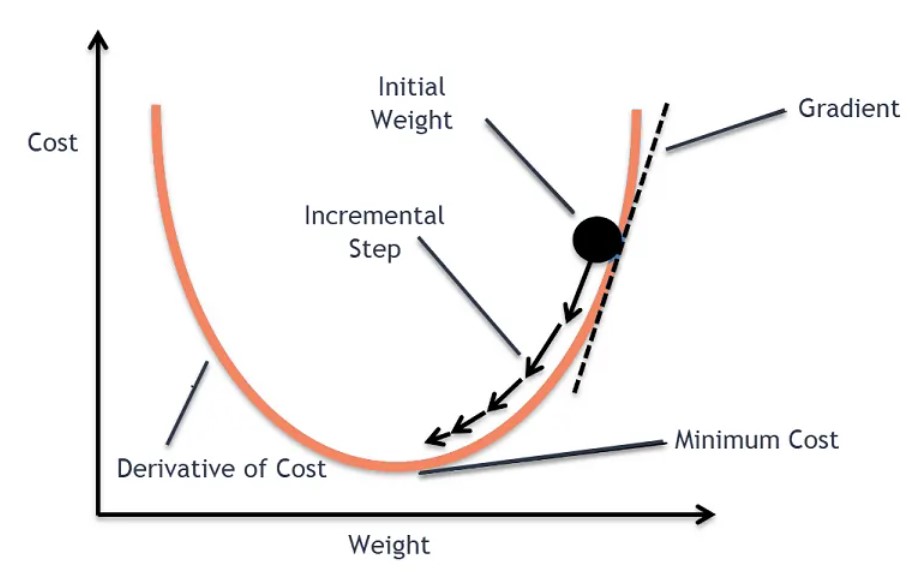
Why We Don’t Use Gradient Descent Algorithm In Linear Regression?
Why We Don’t Use Gradient Descent Algorithm In Linear Regression? Table Of Contents: hI (1) Reason We do apply gradient descent to linear regression, but often it’s not necessary because linear regression has a closed-form solution that is computationally efficient for small to medium-sized datasets. Let me explain: Closed-Form Solution for Linear Regression Here we can directly take the derivative of the Loss function and equate it to zero. Then we can solve the equation to get the optimal value of the beta. How Can We Directly Equate A Single Derivative To Zero To Get The Beta Value. We can
-

Logistic Regression Topics.
Logistic Regression Topics Table Of Contents: Introduction to Logistic Regression Mathematical Foundation Model Fitting Assumptions of Logistic Regression Feature Engineering for Logistic Regression Evaluation Metrics for Logistic Regression Regularization in Logistic Regression Advanced Topics Model Interpretation Practical Considerations Common Problems in Logistic Regression Implementation in Programming Applications of Logistic Regression (1) Introduction to Logistic Regression (2) Assumptions of Logistic Regression (3) Mathematical Foundation (4) Model Fitting (5) Feature Engineering for Logistic Regression (6) Evaluation Metrics for Logistic Regression (7) Regularization in Logistic Regression (8) Extensions of Logistic Regression (9) Challenges and Solutions (10) Advanced Topics (11) Model Interpretation (12) Practical
-

Linear Regression – (R – Squared and Adjusted R – Squared)
R- Squared and Adjusted R-Squared Table Of Contents: What Is R-Squared Value? Formula For R-Squared Value. Interpretation Of R-Squared Value. Example Of R-Squared. Key Points To Note. Conclusion. (1) What Is R-Squared Value? R-squared, also known as the coefficient of determination, is a statistical measure that shows how well the independent variable(s) in a regression model explain the variability of the dependent variable. It provides an indication of the model’s goodness of fit. (2) Formula For R Squared Value (3) Interpretation Of R-Squared (4) Example Of R-Squared (5) Key Points To Note (6) Conclusion (7) Adjusted R-Squared Adjusted R-squared is
-
Linear Regression Topics
Linear Regression Topics Table Of Contents: Basics of Linear Regression Model Components Assumptions of Linear Regression Diagnostics Violations of Assumptions Statistical Concepts Model Evaluation Extensions and Variants Feature Engineering for Linear Regression Advanced Topics (1) Basics Of Linear Regression (2) Assumptions of Linear Regression (3) Model Components (4) Statistical Concepts (5) Diagnostics (6) Extensions and Variants (7) Model Evaluation (8) Violations of Assumptions (9) Feature Engineering for Linear Regression (10) Advanced Topics
-

Linear Regression – Assumption – 5 (Autocorrelation In Regression)
Autocorrelation Table Of Contents: What Is Autocorrelation? Assumption Of No Autocorrelation. Why No Autocorrelation Is Important? Common Causes Of Autocorrelation. Detecting Autocorrelation. Addressing Autocorrelation. Examples Of Autocorrelation In Residuals. (1) What Is Autocorrelation? In linear regression, autocorrelation refers to the correlation of the residuals (errors) of the model with themselves, particularly in time-series data or data with a sequential nature. The assumption of no autocorrelation is one of the key assumptions for the validity of a linear regression model. (2) Assumption Of No Autocorrelation. (3) Why No Autocorrelation Is Important? (4) Common Causes Of Autocorrelation. Omitted Variables: Missing important predictors
-

Linear Regression – Assumption – 4 (Homoscedasticity In Details?)
Homoscedasticity Table Of Contents: What Is Homoscedasticity ? Why Is Homoscedasticity Important? How to Identify Homoscedasticity? Examples Of Homoscedasticity . Consequences of Violating Homoscedasticity. How to Fix Heteroscedasticity? In Summary. (1) What Is Homoscedasticity? Homoscedasticity is an assumption in linear regression that the variance of the errors (residuals) is constant across all levels of the independent variables. In other words, the spread of residuals should be roughly the same for all predicted values of the dependent variable. (2) Why Is Homoscedasticity Important? Homoscedasticity is a key assumption in linear regression because: Accuracy of Predictions: When the variance of residuals is
-

Linear Regression – Assumption – 2 (Inflection Factor.)
Variance Inflection Factor Table Of Contents: What Is VIF? How VIF Works? Mathematical Formula. Interpreting VIF Value. Example Of VIF. Why VIF Is Important? How To Handle High VIF? Summary. (1) What Is VIF? The Variance Inflation Factor (VIF) is a statistical measure used to detect multicollinearity in a regression model. It quantifies how much the variance of a regression coefficient is inflated due to multicollinearity among the independent variables. In simpler terms, VIF helps identify whether a predictor is strongly correlated with other predictors in the model. (2) How VIF Works? If an independent variable is highly correlated with
-

Linear Regression – Assumption – 2 (Effect Of Multicollinearity In Regression Model.)
Effect Of Multicollinearity In Regression Model. Table Of Contents: What Is Multicollinearity? Effects Of Multicollinearity. (1) What Is Multicollinearity? Multicollinearity refers to a situation in multiple regression where two or more independent variables are highly correlated. This means that these variables share a significant amount of the same information, making it difficult for the regression model to separate their individual effects on the dependent variable. Here’s how multicollinearity affects regression coefficients: (2) Effects Of Multicollinearity. 1. Instability of Coefficients When multicollinearity exists, small changes in the data can lead to large changes in the estimated regression coefficients. This happens because
