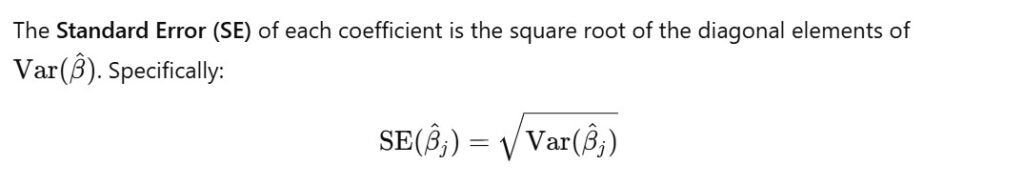Effect Of Multicollinearity In Regression Model.
Table Of Contents:
- What Is Multicollinearity?
- Effects Of Multicollinearity.
(1) What Is Multicollinearity?
- Multicollinearity refers to a situation in multiple regression where two or more independent variables are highly correlated.
- This means that these variables share a significant amount of the same information, making it difficult for the regression model to separate their individual effects on the dependent variable.
- Here’s how multicollinearity affects regression coefficients:
(2) Effects Of Multicollinearity.
1. Instability of Coefficients
- When multicollinearity exists, small changes in the data can lead to large changes in the estimated regression coefficients.
- This happens because the model struggles to determine how much of the shared variance should be attributed to each variable, leading to instability and unreliable coefficients.
2. Inflated Standard Errors
- Multicollinearity inflates the standard errors of the regression coefficients.
- Larger standard errors reduce the statistical significance of the coefficients, making it harder to determine if an independent variable truly has an effect on the dependent variable.
3. Difficulty in Interpretation
- The regression coefficients may not accurately represent the effect of an independent variable on the dependent variable, as they are influenced by the presence of correlated variables.
- This makes it difficult to interpret the individual contributions of the variables.
4.Reduced Predictive Power
- While multicollinearity may not necessarily affect the overall predictive power of the model, it can lead to overfitting and reduced generalizability when applied to new datasets.
5.Variance Inflation Factor (VIF)
- Multicollinearity can be quantified using metrics like the Variance Inflation Factor (VIF).
- A high VIF indicates a high degree of multicollinearity, signaling potential problems with coefficient estimation.
(3) Instability Of Coefficients
(4) Inflected Standard Errors.
Standard Error Of The Coefficients:


Example Of Large Standard Error.



- Calculation Standard Error: