Praudyog

Heart Failure Prediction!

admin

Heart Failure Prediction

Table Of Contents:

  1. What Is The Business Use Case?
  2. Steps Involved In Heart Failure Prediction.
  3. Importing Library
  4. Loading Data
  5. Plotting Count Plot
  6. Examining The Correlation Matrix
  7. For All The Features.
  8. Examining Count Plot Of Age.
  9. Outlier Detection Plotting.
  10. KDE Plot.
  11. Data Preprocessing.
  12. Train Test Split.
  13. Model Building.
  14. Model Conclusion.

(1) What Is The Business Use Case?

  • Cardiovascular diseases are the most common cause of death globally, taking an estimated 17.9 million lives each year, which accounts for 31% of all deaths worldwide.
  • Heart failure is a common event caused by Cardiovascular diseases. It is characterized by the heart’s inability to pump an adequate blood supply to the body.
  • Without sufficient blood flow, all major body functions are disrupted. Heart failure is a condition or a collection of symptoms that weaken the heart.

(2) Steps Involved In Heart Failure Prediction.

  1. Importing Library.
  2. Loading Data.
  3. Data Analysis.
  4. Data Preprocessing.
  5. Model Building.
  6. Conclusion.

(3) Importing Library

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import preprocessing
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import seaborn as sns
from keras.layers import Dense, BatchNormalization, Dropout, LSTM
from keras.models import Sequential
from keras.utils import to_categorical
from keras import callbacks
from sklearn.metrics import precision_score, recall_score, confusion_matrix, classification_report, accuracy_score, f1_score

(4) Loading Data

data = pd.read_csv('heart_failure_clinical_records_dataset.csv')
data.head()
data.info()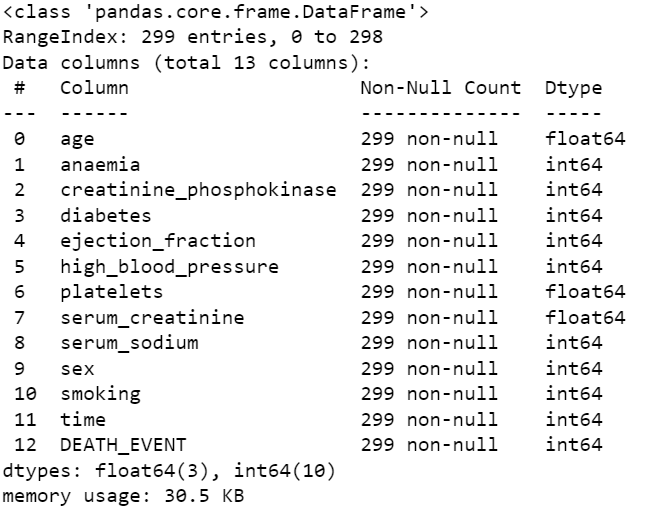

About The Data:

  1. age: Age of the patient
  2. anaemia: If the patient had the haemoglobin below the normal range
  3. creatinine_phosphokinase: The level of the creatine phosphokinase in the blood in mcg/L
  4. diabetes: If the patient was diabetic
  5. ejection_fraction: Ejection fraction is a measurement of how much blood the left ventricle pumps out with each contraction
  6. high_blood_pressure: If the patient had hypertension
  7. platelets: Platelet count of blood in kiloplatelets/mL
  8. serum_creatinine: The level of serum creatinine in the blood in mg/dL
  9. serum_sodium: The level of serum sodium in the blood in mEq/L
  10. sex: The sex of the patient
  11. smoking: If the patient smokes actively or ever did in past
  12. time: It is the time of the patient’s follow-up visit for the disease in months
  13. DEATH_EVENT: If the patient is deceased during the follow-up period.

(5) Plotting Count Plot

  • We begin our analysis by plotting a count plot of the target attribute. A correlation matrix of the various attributes is used to examine the importance of the feature.
cols = ['red', 'blue']
sns.countplot(x = data['DEATH_EVENT'], palette = cols)
  • The point to note is that there is an imbalance in the data.

(6) Examining The Correlation Matrix For All The Features.

cmap = sns.diverging_palette(275, 150,  s=40, l=65, n=9)
corrmat = data.corr()
plt.subplot(figsize = (18, 18))
sns.heatmap(corrmat, cmap = cmap, annot = True, square = True)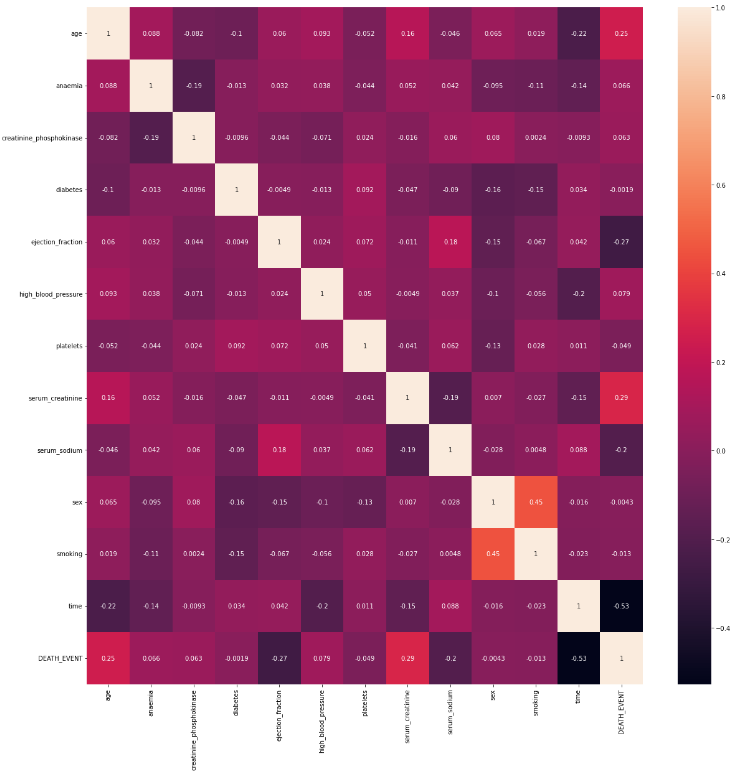

Note:

  • The time of the patient’s follow-up visit for the disease is crucial as the initial diagnosis of the cardiovascular issue and treatment reduces the chances of any fatality. It holds an inverse relation.
  • The ejection fraction is the second most important feature. It is quite expected as it is the efficiency of the heart.
  • The age of the patient is the third most correlated feature. Clearly as the heart’s functioning declines with ageing.

(7) Examining Count Plot Of Age:

#Evauating age distrivution 
plt.figure(figsize=(20,12))
Days_of_week=sns.countplot(x=data['age'],data=data, hue ="DEATH_EVENT",palette = cols)
Days_of_week.set_title("Distribution Of Age", color="#774571")

Note:

  • The above diagram shows the death ratios at particular ages.
  • At age 60 the non-death-to-death ratio is quite significant.

(8) Outlier Detection Plotting:

  • Boxen and swarm plot of some non-binary features.
feature = ["age","creatinine_phosphokinase","ejection_fraction","platelets","serum_creatinine","serum_sodium", "time"]
for i in feature:
    plt.figure(figsize=(8,8))
    sns.swarmplot(x=data["DEATH_EVENT"], y=data[i], color="black", alpha=0.5)
    sns.boxenplot(x=data["DEATH_EVENT"], y=data[i], palette=cols)
    plt.show()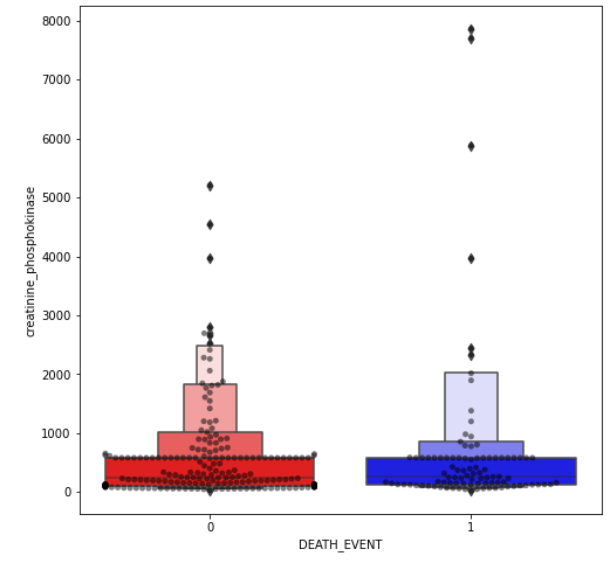

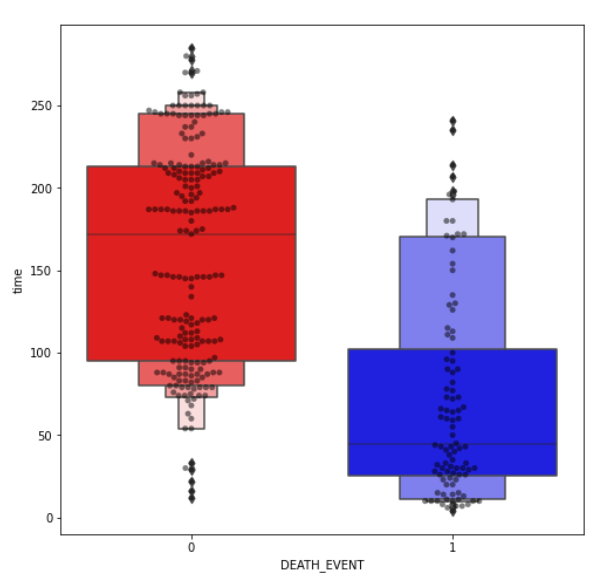
Note:

  • I spotted outliers on our dataset. I didn’t remove them yet as it may lead to overfitting.
  • Though we may end up with better statistics. In this case, with medical data, the outliers may be an important deciding factor.

(9) KDE Plot:

  • Next, we examine the kdeplot of time and age as they both are significant features.
sns.kdeplot(x = data['time'], y = data['age'], hue = data['SEATH_EVENT'], palette = cols)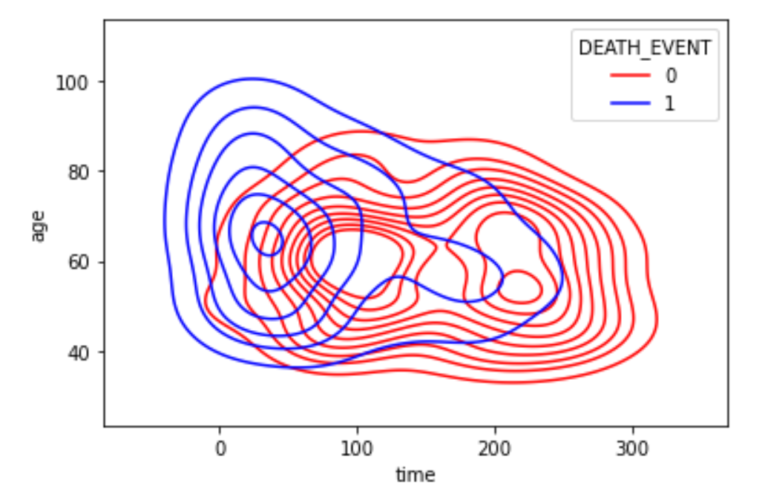

(10) Data Preprocessing:

  • Steps involved in Data Preprocessing 

    • Dropping the outliers based on data analysis
    • Assigning values to features as X and target as y
    • Perform the scaling of the features
    • Split test and training sets

Assigning Values To Features As X And Target As y : 

X = data.drop(['DEATH_EVENT'], axis = 1)
y = data['DEATH_EVENT']

Applying Standard Scalar For The Features:

col_names = list(X.columns)
s_scaler = preprocessing.StandardScaler()
X_df = s_scaler.fit_transform(X)
X_df = pd.DataFrame(data = X_df, columns = col_names)
X_df.head()

Box Plot For Scaled Features:

colours =["#774571","#b398af","#f1f1f1" ,"#afcdc7", "#6daa9f"]
plt.figure(figsize = (20,10))
sns.boxenplot(data = X_df, palette = colours)
plt.xticks(rotation = 90)
plt.show()

(11) Train Test Split:

X_train, X_test, y_train, y_test = train_test_split(X_df, y, test_size = 0.2, random_state = 2)

print('X Train: ', X_train.shape)
print('X Test: ',  X_test.shape)
print('y Train: ', X_train.shape)
print('y Test: ',  X_test.shape)

(12) Model Building:

  • The following steps are involved in the model building

    • Initialising the ANN
    • Defining by adding layers
    • Compiling the ANN
    • Train the ANN

Defining Early Stopping Method:

early_stopping = callbacks.EarlyStopping(
                           min_delta=0.001, # minimium amount of change to count as an improvement
                           patience=20, # how many epochs to wait before stopping
                           restore_best_weights=True
                          )

Model Initialization:

model.sequential()

Adding Dense Layers:

model.add(Dense(units = 16, input_dim = 12, activation = 'relu', kernel_initializer = 'uniform'))
model.add(Dense(units = 8, kernel_initializer = 'uniform', activation = 'relu'))
model.add(Dropout(0.25))
model.add(Dense(units = 4, kernel_initializer = 'uniform', activation = 'relu'))
model.add(Dropout(0.5))
model.add(Dense(units = 1, kernel_initializer = 'uniform', activation = 'sigmoid'))

Model Compilation:

model.compile(loss = 'binary_crossentropy', optimizer = 'adam', metrics = ['accuracy'])

Training The ANN Model:

history = model.fit(X_train, y_train, ebatch_size = 32, epochs = 500, callbacks = [early_stopping], validation_split = 0.2)

Validation Accuracy:

val_accuracy = np.mean(history.history['val_accuracy'])
print("\n%s: %.2f%%" % ('val_accuracy', val_accuracy*100))
history_df = pd.DataFrame(history.history)

history_df

Plotting Training And Validation Loss Over Epochs:

history_df = pd.DataFrame(history.history)

plt.plot(history_df.loc[:, ['loss']], "#6daa9f", label='Training loss')
plt.plot(history_df.loc[:, ['val_loss']],"#774571", label='Validation loss')
plt.title('Training and Validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend(loc="best")

plt.show()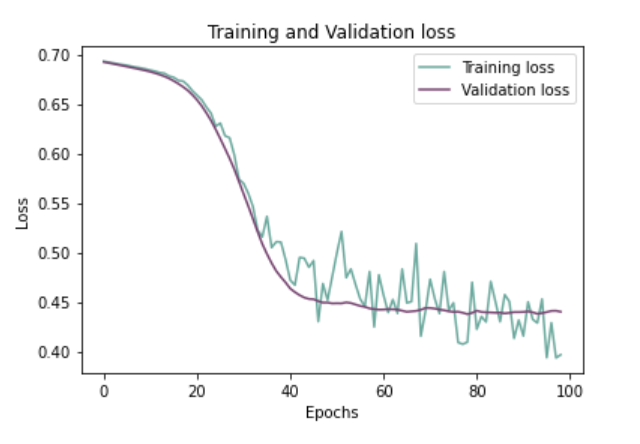

Plotting Training And Validation Accuracy Over Epochs:

history_df = pd.DataFrame(history.history)

plt.plot(history_df.loc[:, ['accuracy']], "#6daa9f", label='Training accuracy')
plt.plot(history_df.loc[:, ['val_accuracy']], "#774571", label='Validation accuracy')

plt.title('Training and Validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()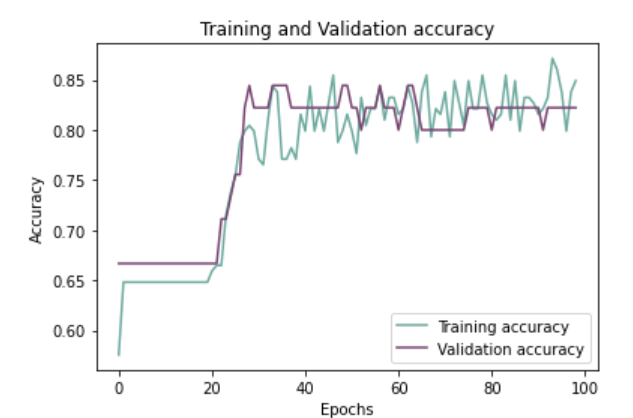

(13) Model Conclusion:

  • Concluding the model with:

    • Testing on the test set
    • Evaluating the confusion matrix
    • Evaluating the classification report

Predicting The Test Set Results:

y_pred = model.predict(X_test)
y_pred = (y_pred > 0.5)
y_pred

Evaluating The Confusion Matrix:

cmap1 = sns.diverging_palette(275,150,  s=40, l=65, n=6)
plt.subplots(figsize = (12, 8))
cf_matrix = confusion_matrix(y_test, y_pred)
sns.heatmap(cf_matrix, cmap = cmap1, annot = True, annot_kws = {'size':15})

Evaluating The Classification Report:

print(classification_report(y_test, y_pred))

Leave a Reply

Your email address will not be published. Required fields are marked *