Self Attention In Transformers
Table Of Contents:
- Motivation To Study Self Attention.
- Problem With Word Embedding.
- What Is Contextual Word Embedding?
- How Does Self-Attention Work?
- How To Get The Contextual Word Embeddings?
- Advantages Of First Principle Above Approach.
- Introducing Learnable Parameters In The Model.
(1) Motivation To Study Self Attention.
- In 2024 we all know that there is a technology called ‘GenAI’ has penetrated into the market.
- With this technology we can create different new images, videos, texts from scratch automatically.
- The center of ‘GenAI’ technology is the ‘Transformers’.
- And the center of the Transformer is the ‘Self Attention’.
- Hence we need to understand ‘Self Attention’ better to understand others.

(2) Problem With Word Embedding.
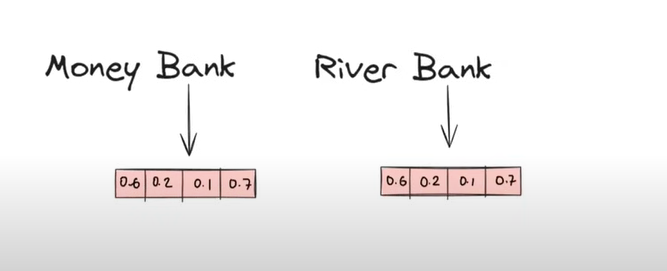
- The problem with the word embedding is that it doesn’t capture the contextual meaning of the word.
- In the above example, we can see that the meaning of ‘Bank’ is different in different sentences.
- But if we are using a word embedding technique the vector representation [0.6, 0.2, 0.1, 0.7] is the same for the word ‘Bank’, which is wrong.
- Hence we need to come up with a new technique that will capture the contextual meaning of the word.
(3) What Is Contextual Word Embedding ?
- Based on the words before and after we need to derive the meaning of the word.
- In the above example ‘River Bank’, the meaning of the word ‘Bank’ will be derived by using its previous and after words, in this case using the word ‘River’.
- In case of ‘Money Bank’ , meaning of Bank will be derived from the word ‘Money’.
(4) How Does Self Attention Works?

- Step-1: The first step is to calculate the static word embedding of the words by using the “Word2Vec” or “glove” technique.
- Step-2: The second step is to pass the static embeddings into an “Self Attention” model.
- Step-3: Finally get the Dynamic Contextual Embedding of the words.
(5) How To Get The Contextual Word Embeddings ?
- In the above example, we can see that the word ‘Bank’ is being used in different contexts.
- Unfortunately, if we use word embedding the meaning of ‘Bank’ will be the same in both of the sentences.
- We need to change the meaning of ‘Bank’ based on the context around the world.
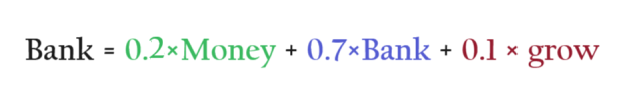
- If I write the Bank embedding as the weighted sum of the words around it, I can capture the context meaning of the word ‘Bank’.
- Because I am taking account of all the surrounding words of the ‘Bank’.
- The numbers [0.2, 0.7, 0.1] represent word similarity.
- ‘Bank’ is 0.2 per cent similar to the word ‘Money’.
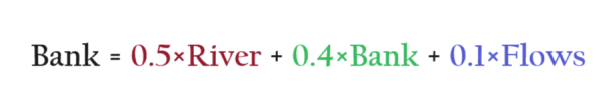
- We can also write the ‘Bank’ equation for the second sentence as above.
Note:
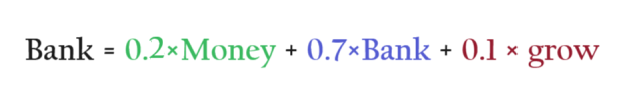
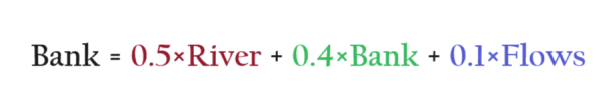
- Automatically the meaning of ‘Bank’ will come as different in both of the sentences.
- It also depends on the context of words.
Cont..
- Let us write each word as the combination of its context words.

- If you focus on the word ‘Bank’ the LHS part is the same but the RHS is different now.
- The computer can’t understand the words hence we need to convert each word in the sentence to a vector format.

- All these numbers on the RHS side represent the similarity between the words.
- So the next question will be how to calculate the similarity between words.
How To Calculate Similarity Between Words?
- The best way to calculate the similarity between words is to calculate the dot product between two vectors.
- First, represent the words in vector format and determine the dot product between the two.
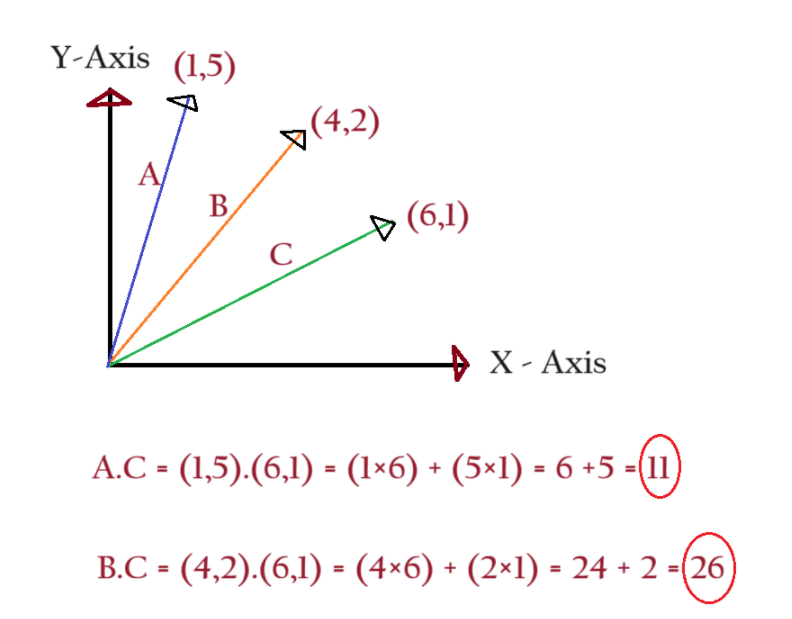
- The dot product of two vectors will be a scalar quantity.
- The dot product of the ‘B’ & ‘C’ vector is 26 and ‘A’ and ‘C’ is 11.
- Hence vectors ‘B’ and ‘C’ are more similar compared to ‘A’ and ‘C’.
- Hence the numbers in the equation represent the similarity between words.
- We can also write the equation for the new embedding as below.

Step-1:
- The new embedding of the word ‘Bank’ is represented in equation format above.
- Diagrammatically we can also represent the above equation as follows.
- Here we are calculating the new embedding of the word ‘Bank’.
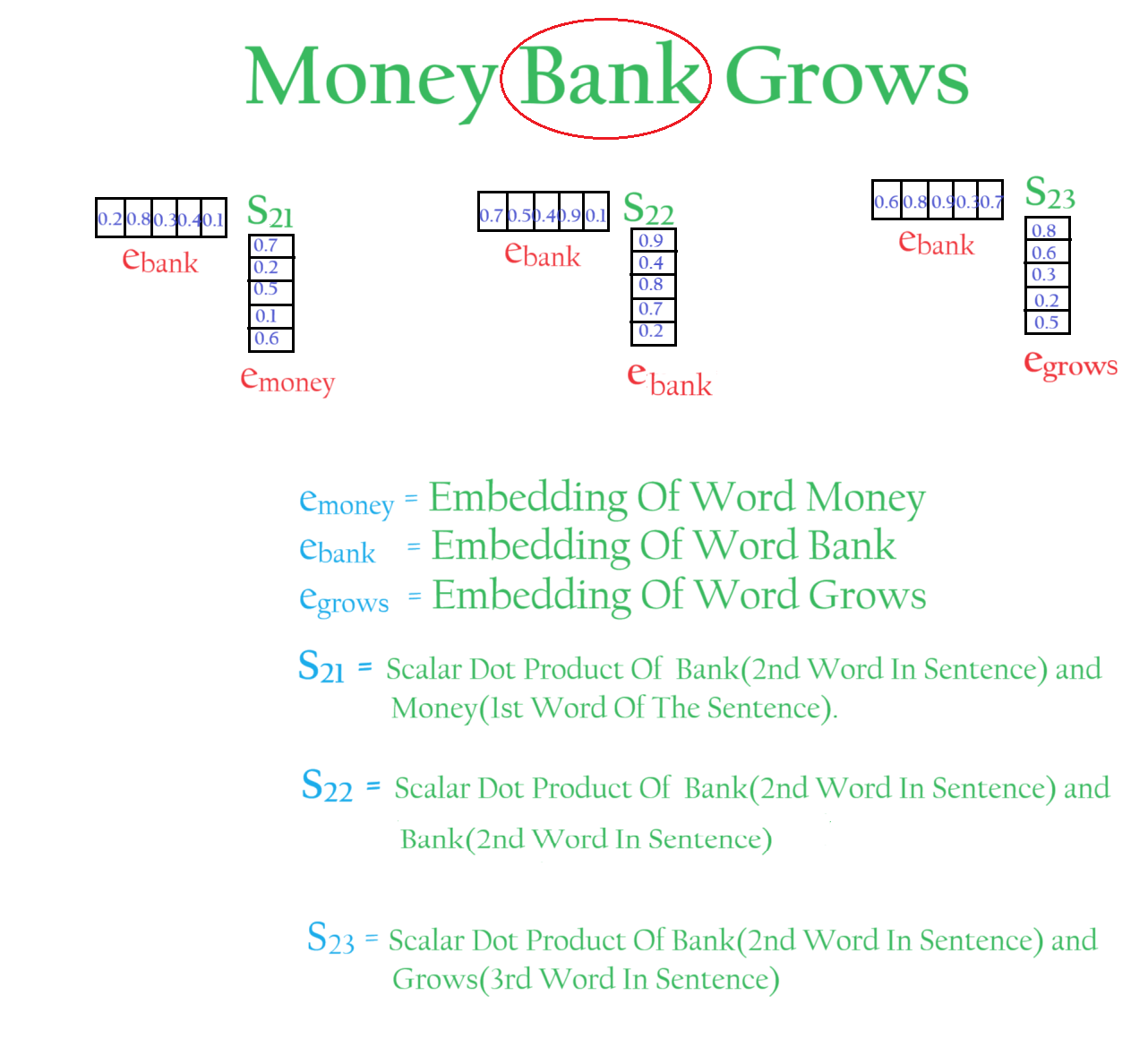
Step-2:
- The dot product result can be of any numeric value but we need to normalize the values so that the sum can be 1.
- There are chances of getting a negative value also hence we will pass the normalized sot product values to a Softmax function.
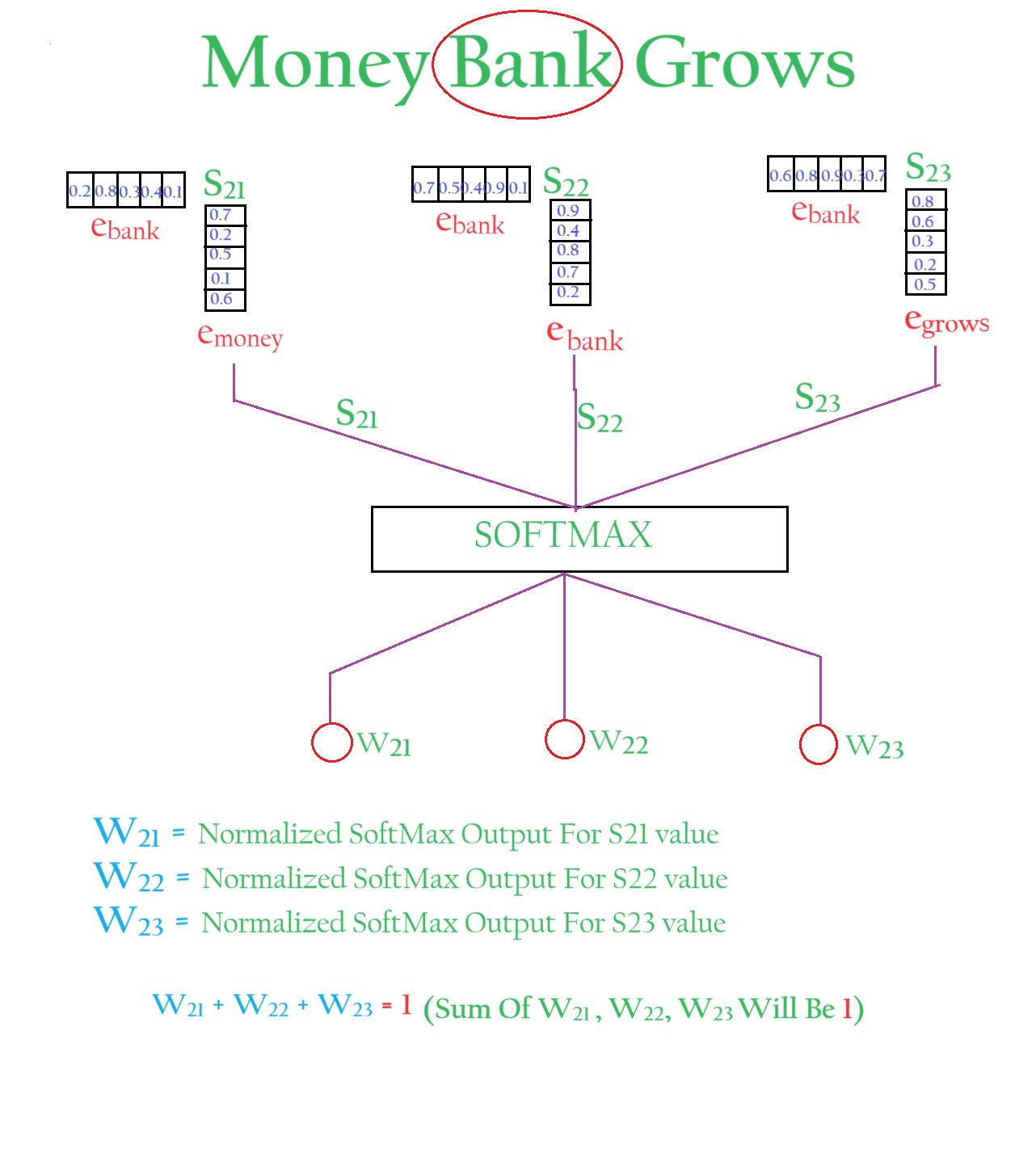
Step-3:
- The normalized dot product values (W21, W22, W23) are multiplied with the individual word embedding values (e(money), e(bank), e(grows)).
- After multiplying the dot product and the word embedding values we finally sum it together to get the new “Contextual Word Embedding” value.
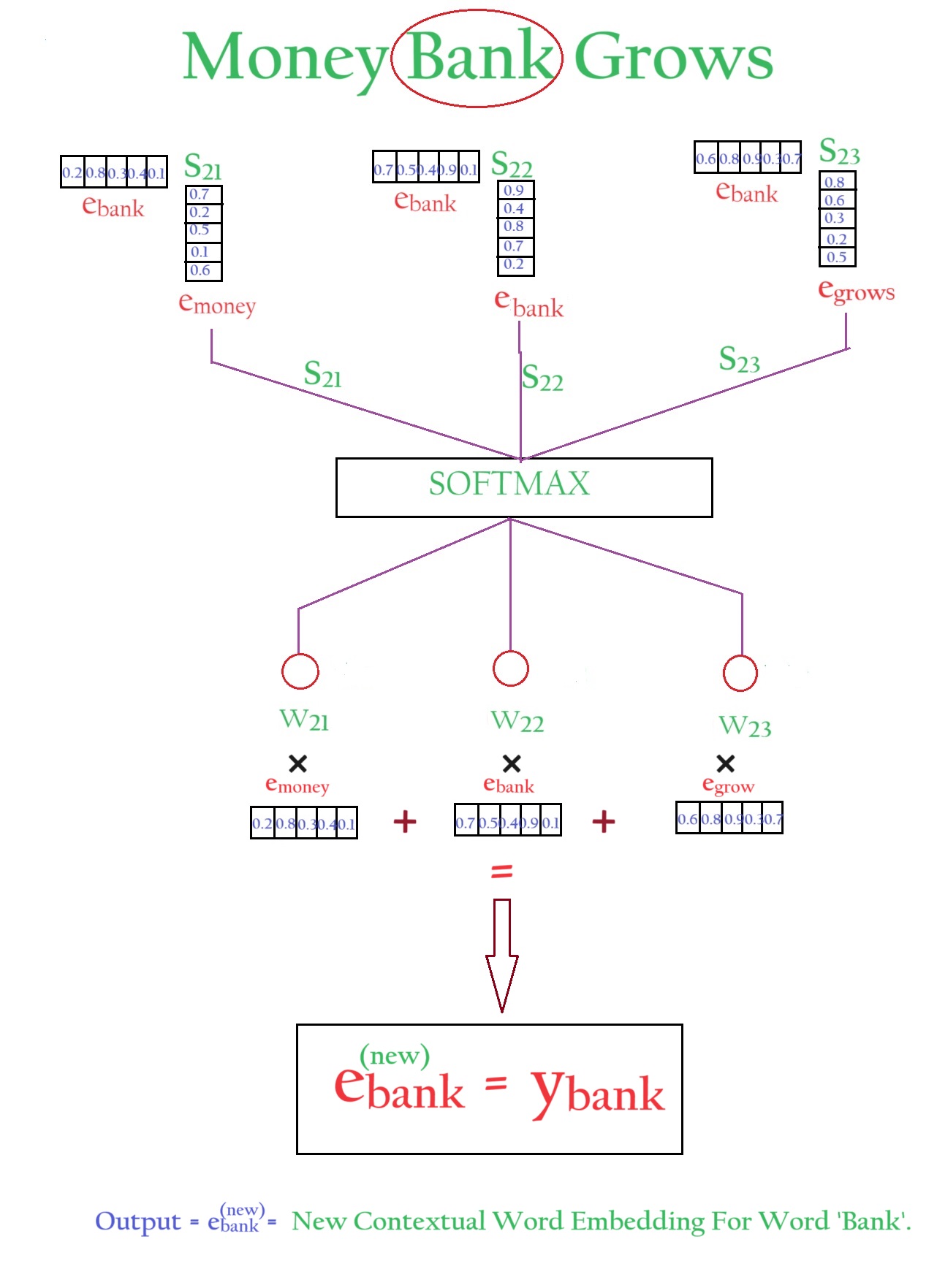
- In this way, we need to find out Ymoney and Ygrows Contextual Word Embedding values.
(6) Advantages Of First Principle Above Approach.
- There are mainly two advantages of this approach.
- This operation is Parallel operation.
- There are no parameters involved.
Parallel Operation Advantage:
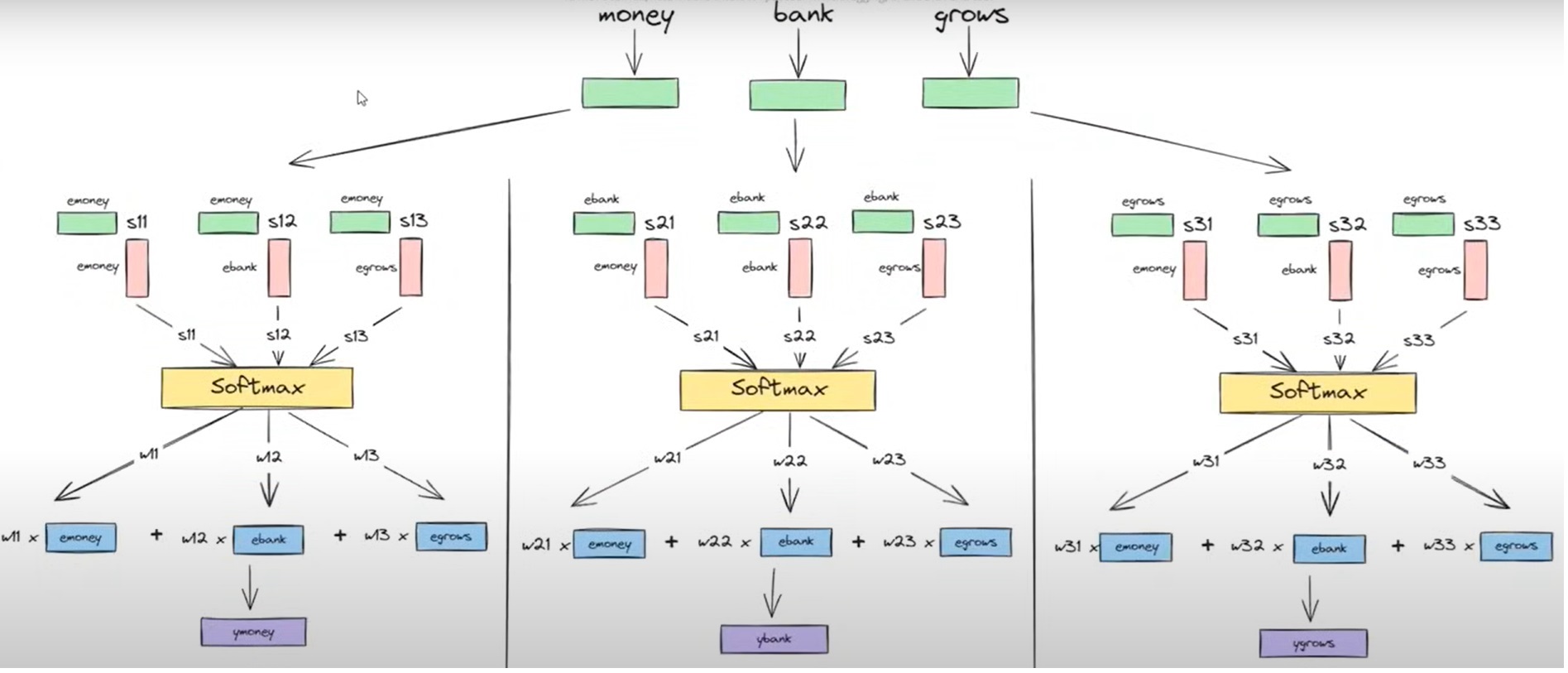
- We can generate the contextual word embedding values of each word parallelly.
- From the above diagram, we can see that there is no operation which is dependent on each other
- Initially, only we need the word embeddings of individual words which we can get at a time.
- If the sentence has thousands of words also we can do this operation parallelly.
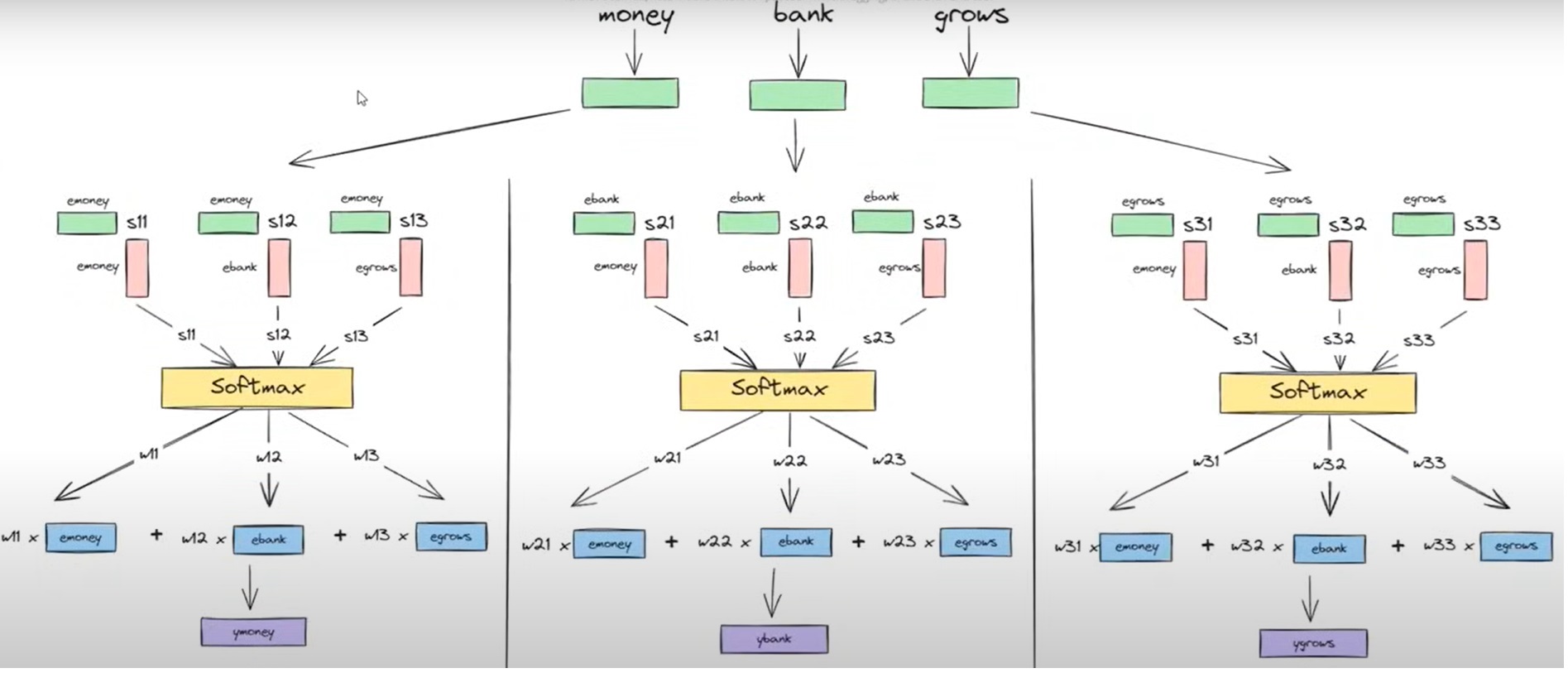
- The above operations we can represent in matrix format as below.
Step-1: Embedding Metrics
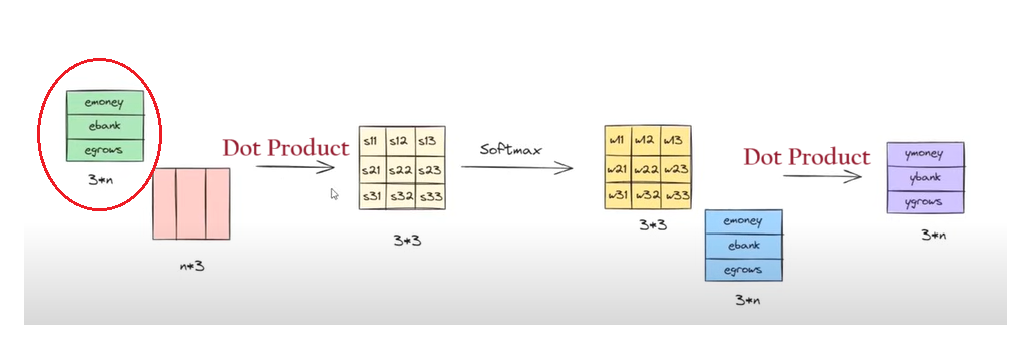
- The first step of our operation was to calculate the dot product of the two-word vectors to find out the similarity between words.
- The above-rounded matrix represents the word embeddings of each word which is of the size 3*n.
- Where 3 = represents the number of words in the sentence.
- n = Represents the number of dimensions of word embedding value. It can be of any value.
Step-2: Transpose Metrics
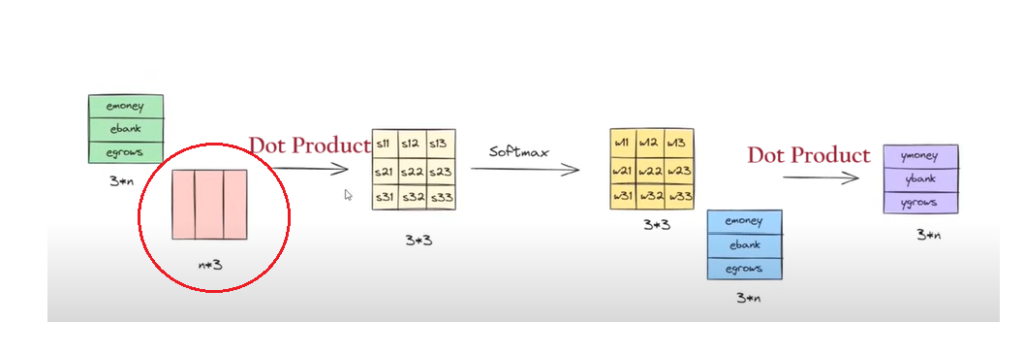
- The above red-rounded metrics represent the transpose vector of each word.
- It will be of size n*3.
Step-3: Dot Product Metrics
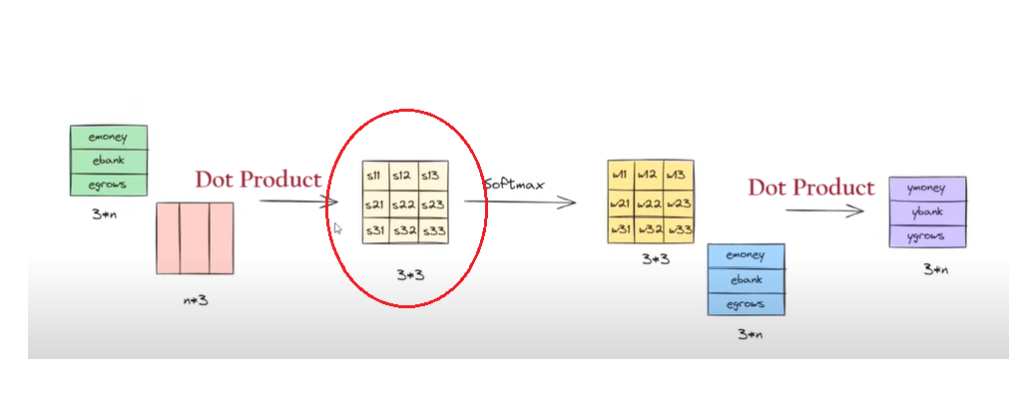
- The above red-rounded metrics represent the dot product of the first two metrics.
- It will be of size 3*3.
Step-4: SoftMax Operation
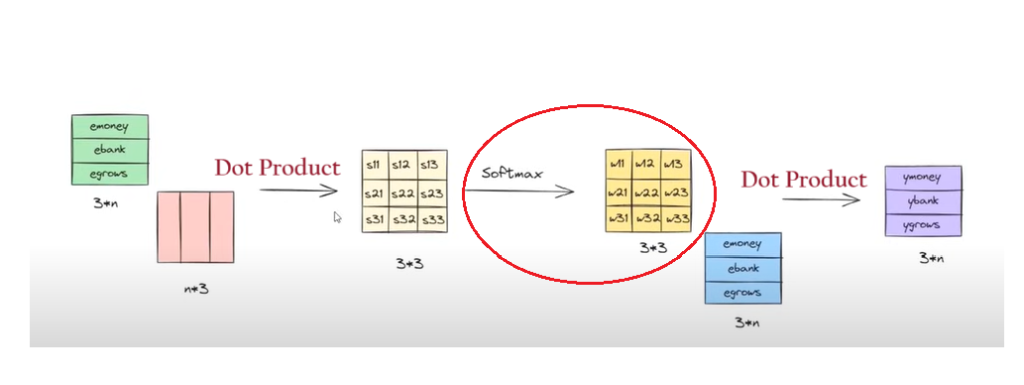
- The dot product metrics will be passed to the softmax function to normalize the values between 0 and 1.
- The output metrics from the SoftMax function will be metrics of size 3*3.
Step-5: Multiplication & Summation
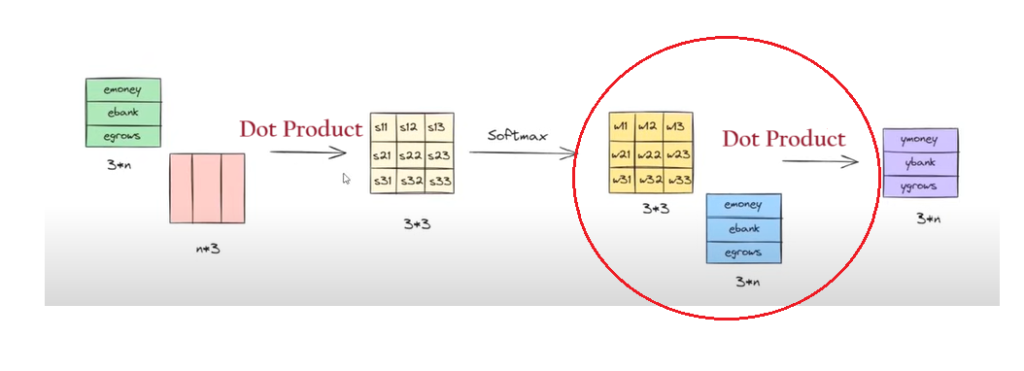
- Finally, the SoftMax output value and the individual word embedding values are multiplied and taken sum together to form the final ‘Contextual Word Embedding Values’.
Note:
- One demerit of parallel processing is that you will lost the sequential information of the sentence.
There Are No Parameters Involved Advantage:
- There are no learning parameters involved in this case, usually, we have learning parameters involved (weights & biases) in the Deep Learning models but here we don’t have them.
- In our above approach, we are performing only three operations matrix dot product, SoftMax operation and Matrix Addition operation.
Note:
- The main problem with this approach is that the word embedding value only depends on the current words of the sentence.
- This is called General Contextual Embedding and not task-specific Contextual embedding.
- Suppose we have English to Hindi translation use case,
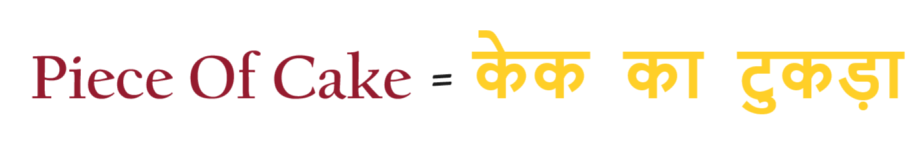
- If we use ‘General Word Embedding’ the translation will be, केक का टुकड़ा.
- But in our data set, we have the translation as सरल काम.
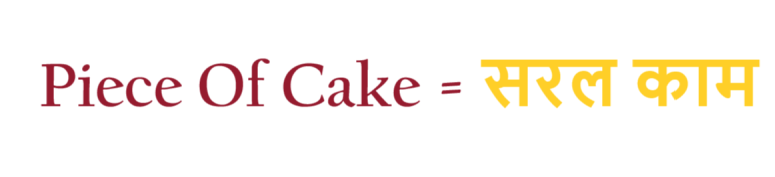
- As we are using General Contextual Embedding the translation will always be केक का टुकड़ा.
- It would never be सरल काम.
- Our model can’t think of this as an output.
Solution:
- The solution to this problem is the task-specific Contextual Embedding.
- This means that we need to train our model on the data set available for the task.
- That means we need to add learning parameters to our model.
(7) Introducing Learnable Parameters In The Model.
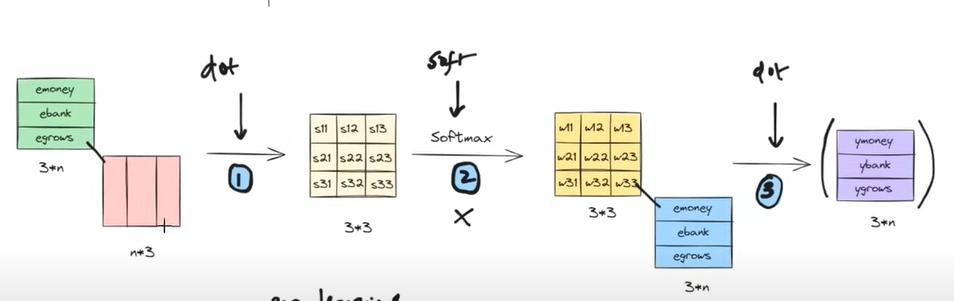
- The question is now where to introduce the weights and biases in the model ?
- There are three places where it is producing some outputs.
- The first one is the dot product output, the second one is the softmax output and the third one is the dot product output.
- SoftMax output doesn’t need any learnable parameters to be introduced because it is just a straight forward operation.
- Hence there are two places left to introduce the learnable parameters.
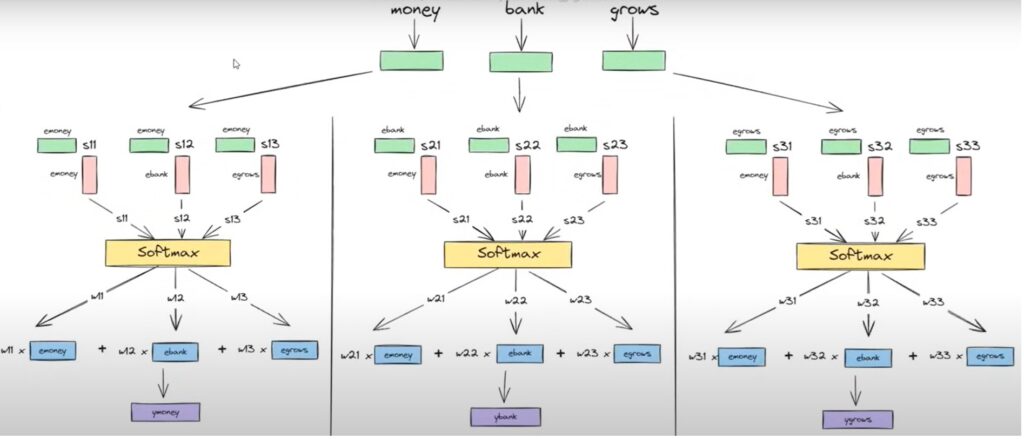
- Let us analyze the above diagram to see where can we introduce the weights and biases.
- From the above diagram, we can see that each word embedding plays 3 different roles in the entire process.
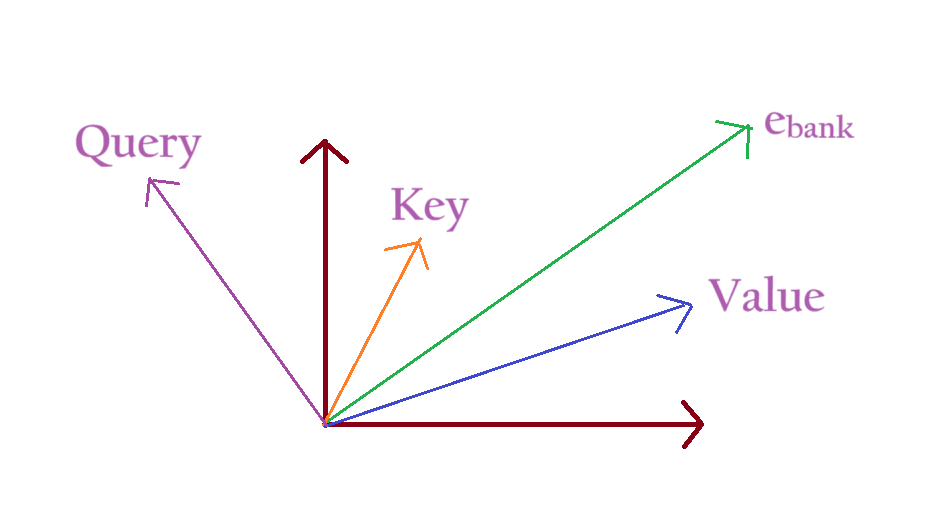
Role-1: Query
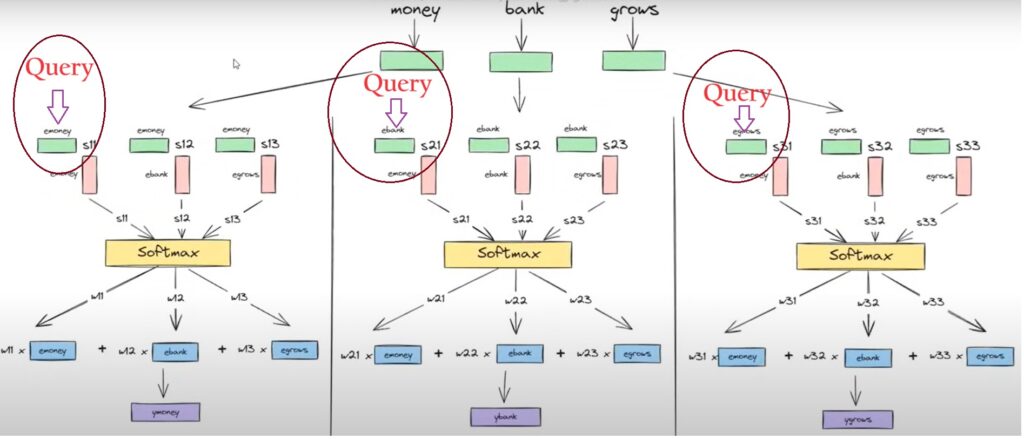
- Our first operation is the dot product where we determine the similarity between words.
- The role of the first embedding is to find out the similarity between words.
- It is asking the question what is the similarity between words?
- Let us call the green boxes as ‘Query’.
Role-2: Key
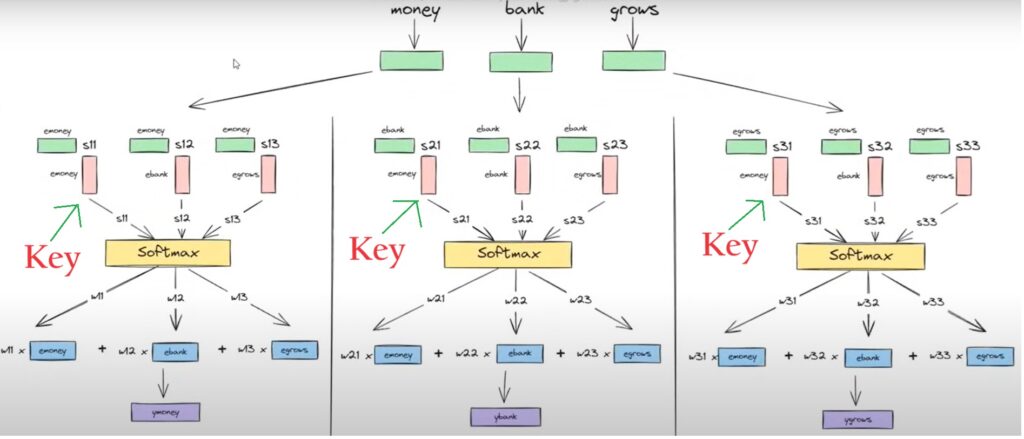
- When the green boxes ask the question, what is the similarity between words?
- The pink box replays by giving the similarity score.
- The pink boxes act as “keys” to whom you can ask questions.
Role-3: Values
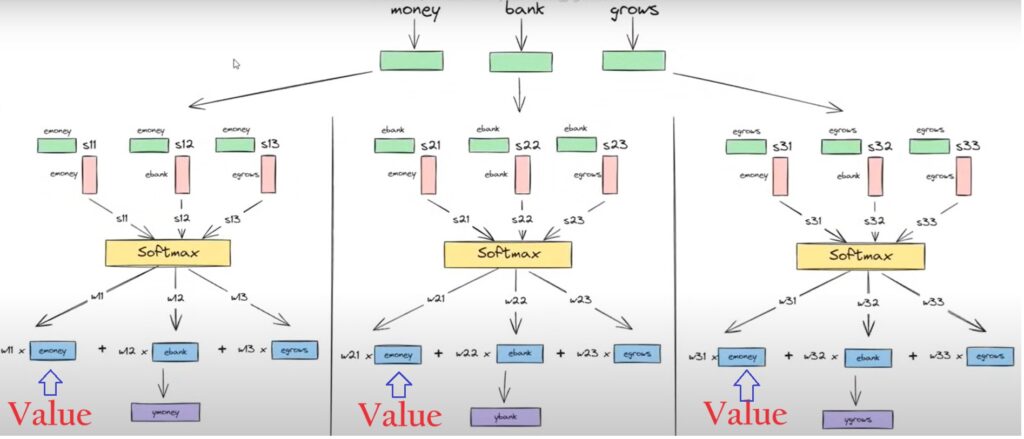
- After our weights are calculated we calculate the weighted sum of the word embeddings, to get the final output.
- To calculate the weighted sum the blue boxes act as “values”.
Where The Concept Of Key, Values Come ?
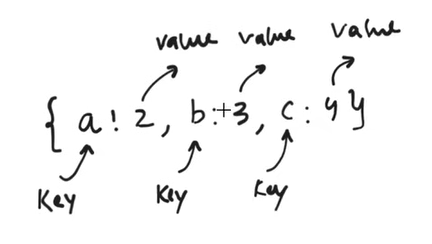
- In Python, we have the concept of key and value pair in Dictionary.
- We will search the dictionary by using its keys.
- dict[a] will be = 2.
- Query: The embedding that asks questions like What is the similarity between words? It is called ‘Query’.
- Key: The embedding that answers the questions is called ‘Keys’.
- Value: The answer to the question is called ‘Value’.
Conclusion:
- We use our word embeddings in three different ways.
- As ‘Query’, ‘Key’ & ‘Value’.
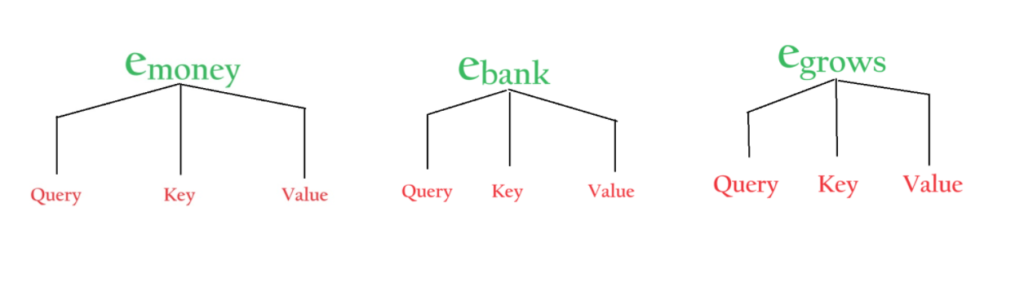
- The problem here is that the same vector becoming ‘Key’, ‘Value’ & ‘Query’.
- The idle case should be like from the single vector we should generate three different vectors.
- One will play the role of ‘Query’, 2nd one will play the role of ‘Key’ and 3rd one as ‘Value’.
- Why should we generate separate vectors?
- The answer is ‘Separation Of Concerns’.
- It is not idle to put an entire load on a single vector.
- A single vector can’t play the role of three different vectors.
- If I transform the single vector into three different vectors there is a chance that each vector will play its role perfectly.
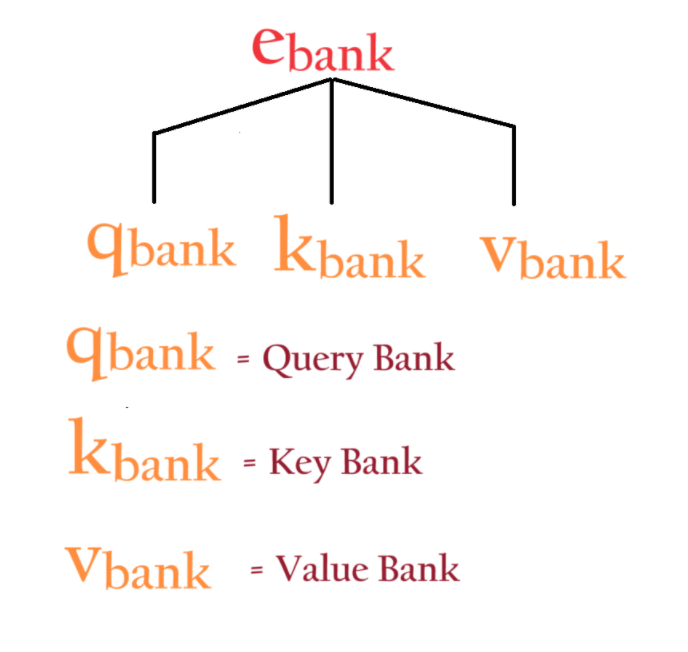
- The question now is how to get the Query, Key and Value vectors.
- The answer is we will train our model with respect to data and our model will learn the representation.
How To Build Three Separate Vectors From Embedding Vector ?
- The question now is how to get the Query, Key and Value vectors from a single vector.
- The question here is, how to convert a single vector to 3 different vector. One of the approach is to use the linear transformation technique.
- We need to multiply our original vector to 3 different metrics to get 3 different vectors.
- The answer is we will train our model with respect to data and our model will learn the representation.
- From the above diagram, you can see that instead of using the original embedding vector, we are using its three component vectors.
- The Component vectors are the ‘Query’, ‘Key’ and ‘Value’ vectors.
- What is the mathematical operation that will give us the three new vectors from a single vector?
- You can create a new vector from the original vector by changing its magnitude(Increase or Decrease), second is a linear transformation.
- Linear transformation means we will multiply the original vector with a metric to get a new vector. Hence its magnitude and direction will change.
- Only scaling will not do any good to our vector we need to perform a Linear Transformation operation to get a new vector.
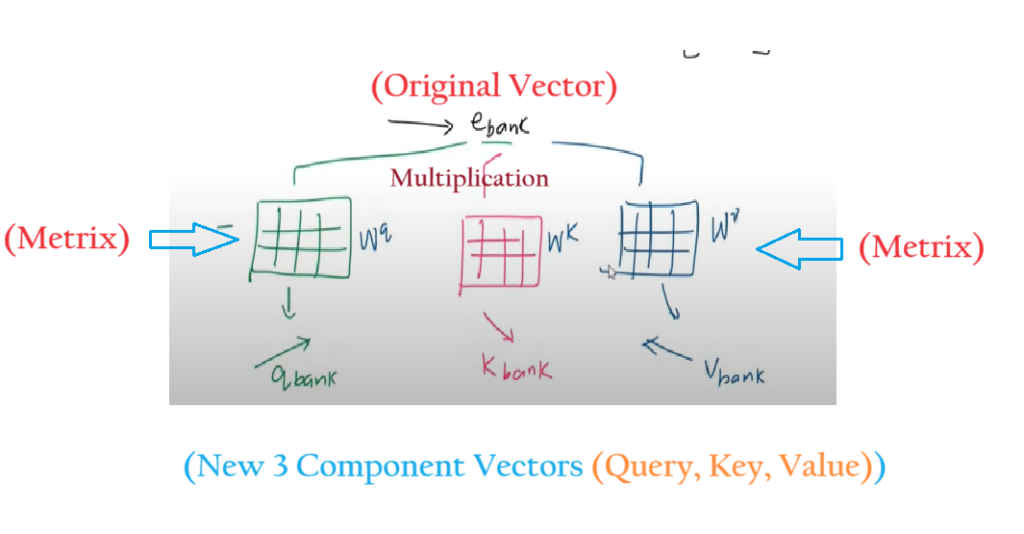
- From the above diagram, we can see that we are multiplying the original vector with three different metrics vectors to get the 3 component vectors.
- Now the question is how to get the metric numbers ?
- The answer is it will be decided from the training data set itself.
- We manually will not decide the values in the matrix.
- We will use our training dataset to train our model and its values will be updated accordingly.
- Let’s understand how it works.
- We will start with the random values of the matrix.
- Suppose the word ‘Bank’ has generated some ‘Query’, ‘Key’ and ‘Value’ vectors.
- On the basis of this, we got one translation and we found some errors.
- We did back propagation due to this the weights of the matrix were changed.
- For the next sentence, we used the updated weights and got the results.
- Like this, we will update our weights until we get the perfect weights with less error.
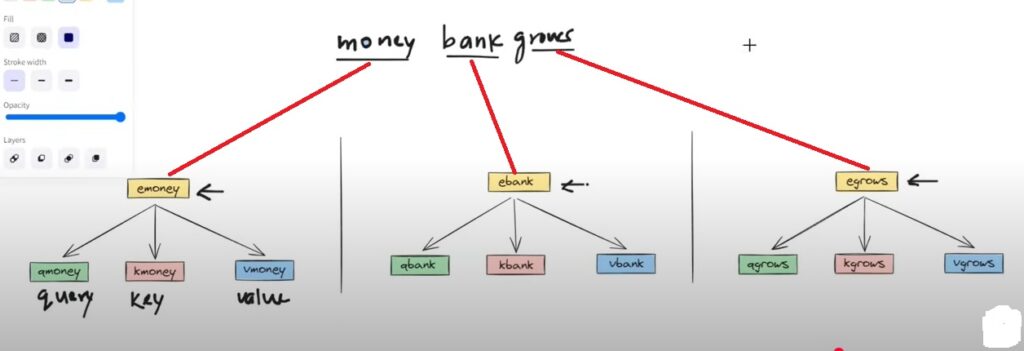
- From the above image you can see that , if we have a sentence “Money Bank Grows” , for each word like ‘Money’, ‘Bank’, and ‘Grows’ we can convert into 3 component vectors.
- Once we got the 3 component vectors then we can use them in our operation.

- Lets find out the contextual embedding for the word ‘Money’.
- We can replace now the ‘Qmoney’, ‘Kmoney’ and ‘Vmoney’ with the newly derived component vectors.
- Money = ( Qmoney + Kmoney + Vmoney )
Problem Statement:
- Derive contextual word embedding for the below sentence words.
- Sentence = “Money Bank Grows”.
- Contextual Embedding Of Money = ?
Solution:
- Step-1: First thing is to derive the matrices for Query, Key and Value vector from the training.
- From the training process we will get the 3 different matrices .

- Step-2: Second is to perform the product of the matrix(scalar) and static embedding vector
- This will result you a vector as as an output.
- This product will give you the 3 component vectors

- Step-3: Get the intermediate component vectors.
- After doing the dot product of the static embedding vector wit the 3 component matrices we will get the 3 separate component vectors for each word.
Money

Bank

Grows

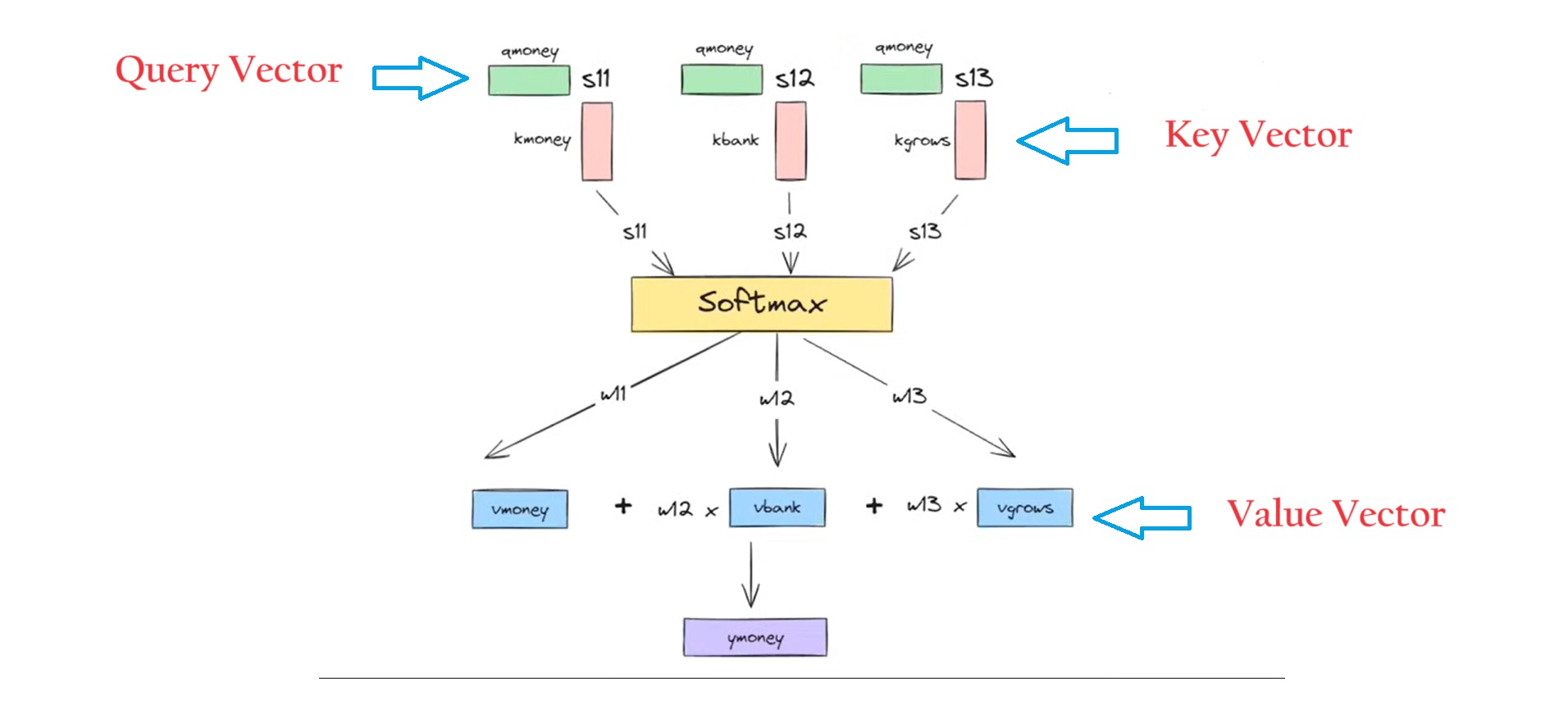
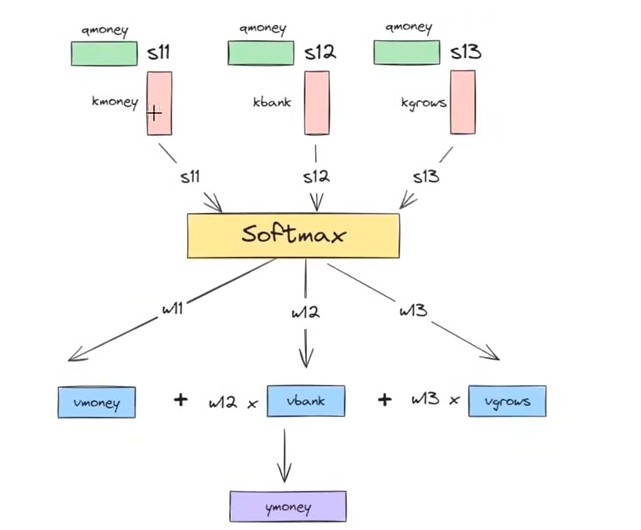
- Step-5: Use this component vectors to get the dot product like Qmoney and Kmoney.
- This dot product will give you a scalar quantity which is “S11”
- Similarly Find the dot product of Qmoney with Kmoney, Kbank and Kqrows vectors.
- This will result you “S12” and “S13”.
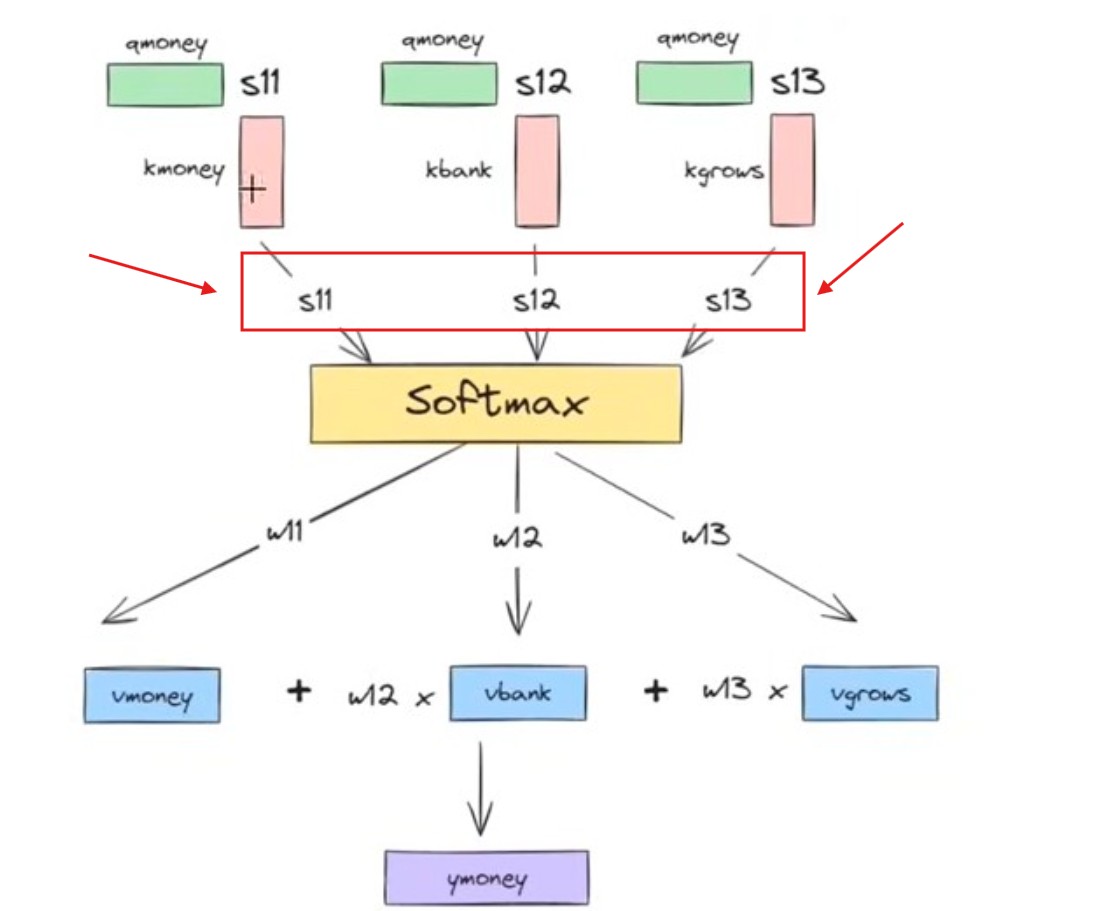
- Step-5: Pass [S11, S12, S13] to the softmax function to get normalize.
- This will give you (W11, W12, W13) scalar quantiaty.
- W11 + W12 + W13 = 1

- Step-5: Now take the weighted sum of the value vector with the weight scalar.
- W11 * Vmoney + W12 * Vbank + W13 * Vgrows = Y money
- Finally we will get the contextual word embedding of the word ‘Money’.
(8) Formula For Self Attention
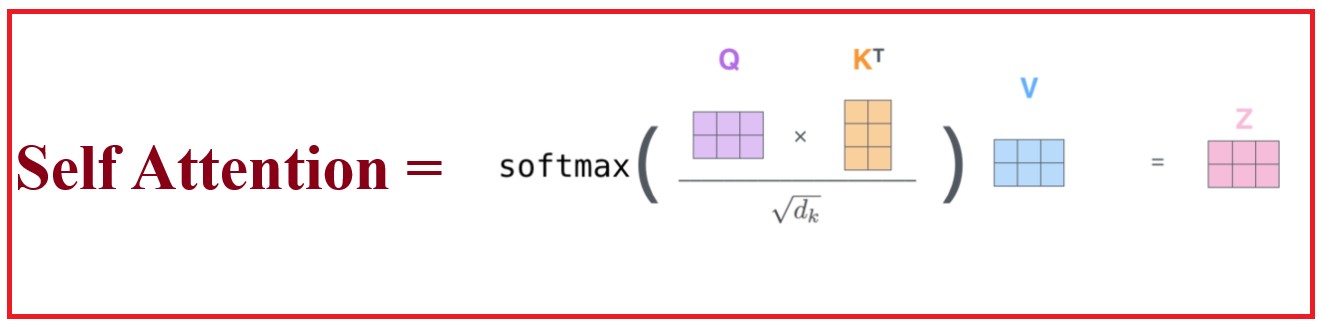

- The output from the self attention will be the context vector for a particular word.
- If you pass a static word embedding to the self attention it will give you the contextual word embedding.
- Input will be static word embedding and the output will be the contextual word embedding.

