Praudyog

Linear Regression – Assumption – 2 (How To Detect & Avoid Multicollinearity ?)

admin

Linear Regression – Assumption- 2 (How To Detect & Avoid Multicollinearity ?)

Table Of Contents:

  1. How To Detect Multicollinearity In The Dataset ?
    • Correlation Matrix.
    • Variance Inflection Factor
    • Model Behavior Observation.
  2. How To Avoid Multicollinearity In The Dataset ?
    • Remove One of the Correlated Variables
    • Use Principal Component Analysis (PCA)
    • Use Regularization Techniques (Ridge/Lasso)

(1) How To Detect Multicollinearity In The Dataset?

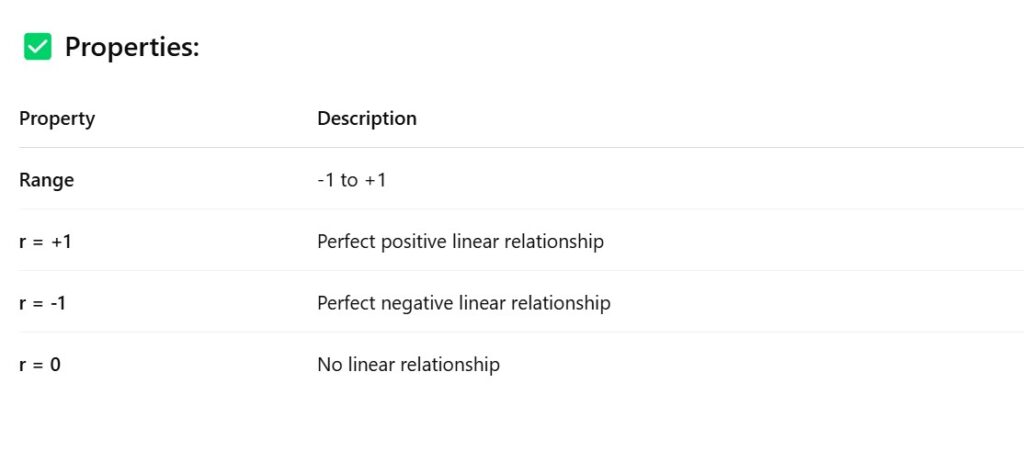
Method – 1: Correlation Matrix (Pearson correlation)

  • We will use Pearson ‘r’ Correlation Coefficient to find the correlation between two variable.
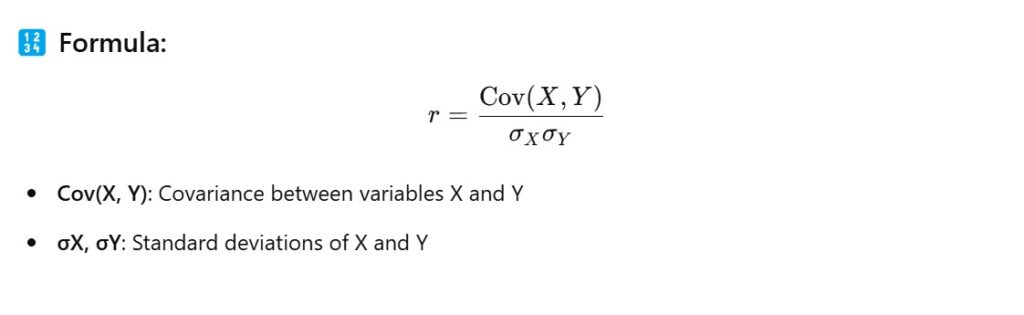
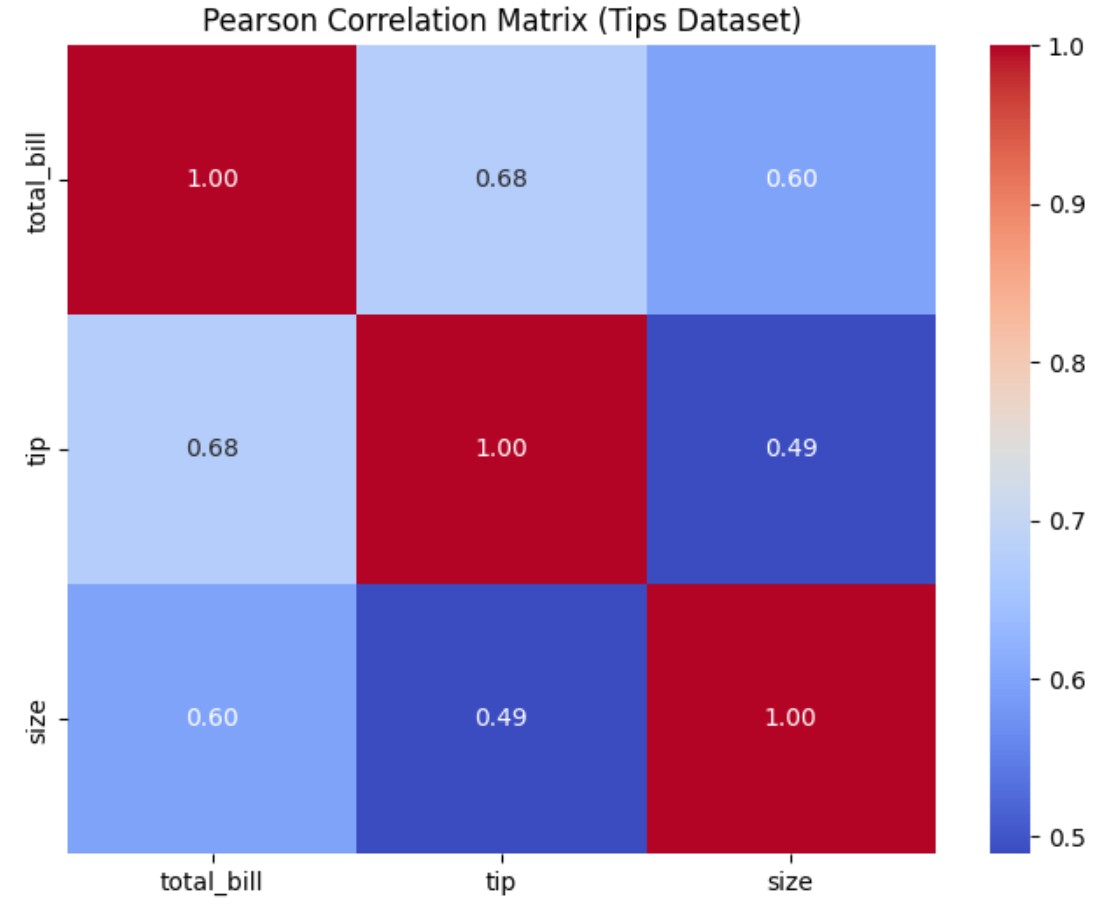
import seaborn as sns
import matplotlib.pyplot as plt

# Load dataset
tips = sns.load_dataset("tips")

# Compute the Pearson correlation matrix
corr_matrix = tips.corr(numeric_only=True)

# Create heatmap
plt.figure(figsize=(8, 6))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt=".2f")

# Styling
plt.title("Pearson Correlation Matrix (Tips Dataset)")
plt.show()

Method – 2: Variance Inflation Factor (VIF)

import pandas as pd
import seaborn as sns
import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor

# Load dataset
tips = sns.load_dataset('tips')

# Select relevant numerical features (exclude categorical)
df = tips[["total_bill", "tip", "size"]]

# Add a constant term for intercept
df_with_const = sm.add_constant(df)

# Calculate VIF for each feature
vif_data = pd.DataFrame()
vif_data["Feature"] = df_with_const.columns
vif_data["VIF"] = [variance_inflation_factor(df_with_const.values, i)
                   for i in range(df_with_const.shape[1])]

print(vif_data)
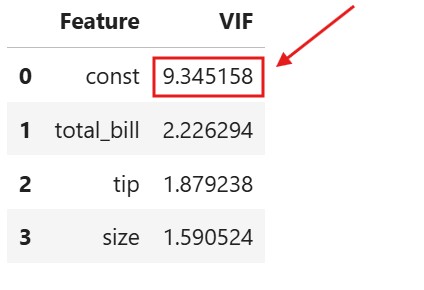
  • Why we use the lower limit as 5 and upper limit as 10 ?
  • For VIF = 5, R-Squared = 0.80, which means 80 % of the variance present in the dependent variable is explained by all the independent variable.
  • For VIF = 10, R-Squared = 0.90, which means 90 % of the variance present in the dependent variable is explained by all the independent variable.

Method – : Model Behavior

  • You have two features, X1 and X2, that are highly correlated. They’re both providing very similar information to the model.
  • So when the model fits: It’s hard to know how much weight (coefficient) to give to X1 and X2, because changing one’s value affects the other.
  • This causes multicollinearity, and the model starts “splitting the credit” between them in a shaky way.
  • Note: After giving the unstable weights to the two variable, if you remove one variable (x2) its credit or contribution will go to other correlated variable (x1).
  • Hence its weight will drastically increase or decrease. With a large unit.
  • Question: Now the question is why the weight not got distributed to other non correlated variable ?
  • Answer: X1 and X2 shared a lot of overlapping info. When you remove X2, that info still exists in X1. So the model naturally adjusts the coefficient of X1 to account for that extra explanation. It’s not that the effect “jumps” to X1, but rather that the shared information already exists in X1 — so the model just leans more heavily on it.

  • Only the unique variance that was explained only by X2 (and not by X1) gets pushed to the residual/error term.

  • But if X1 and X2 are, say, 90% correlated, then removing X2 doesn’t hurt the model much — because X1 is doing almost the same job.

(2) How To Avoid Multicollinearity In The Dataset ?

Method – 1: Remove One of the Correlated Variables

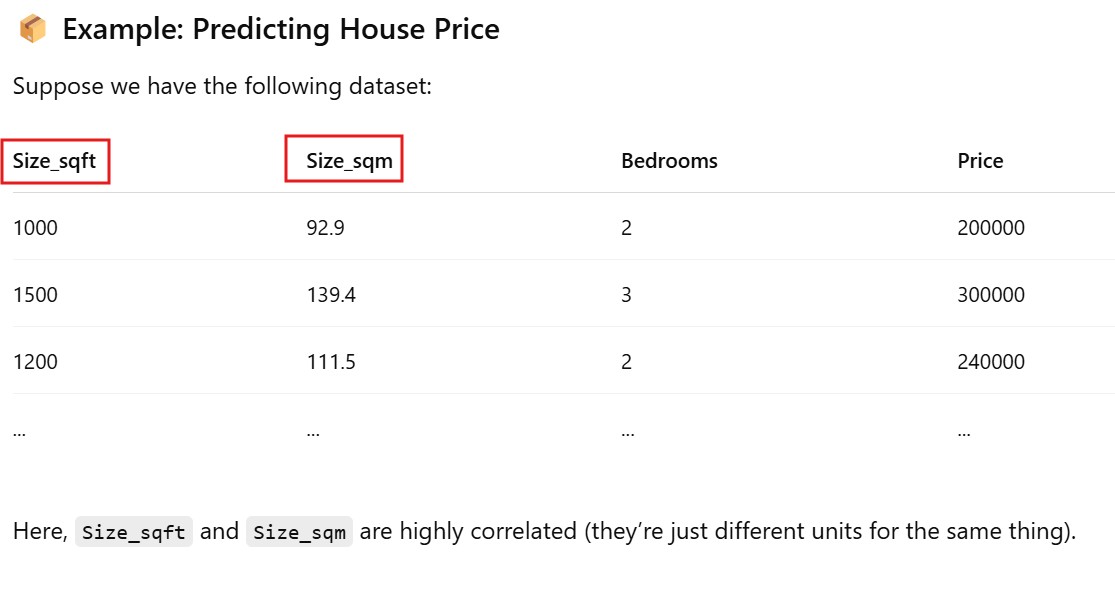
  • Best When: Two or more variables have high correlation (Pearson’s r > 0.7 or VIF > 5/10), and you can justify removing one based on domain knowledge.
import pandas as pd
from statsmodels.api import OLS, add_constant
from statsmodels.stats.outliers_influence import variance_inflation_factor

# Sample data
data = pd.DataFrame({
    'Size_sqft': [1000, 1500, 1200, 1800, 1600],
    'Size_sqm': [92.9, 139.4, 111.5, 167.2, 148.6],
    'Bedrooms': [2, 3, 2, 4, 3],
    'Price': [200000, 300000, 240000, 360000, 320000]
})

# Features and target
X = data[['Size_sqft', 'Size_sqm', 'Bedrooms']]
y = data['Price']

# Add constant
X_const = add_constant(X)

# Check VIF
vif = pd.DataFrame()
vif["VIF"] = [variance_inflation_factor(X_const.values, i) for i in range(X_const.shape[1])]
vif["Feature"] = X_const.columns
print(vif)

# Drop one of the correlated features
X_reduced = data[['Size_sqft', 'Bedrooms']]  # Removed 'Size_sqm'

# Refit model or calculate new VIF
X_const = add_constant(X_reduced)
vif = pd.DataFrame()
vif["VIF"] = [variance_inflation_factor(X_const.values, i) for i in range(X_const.shape[1])]
vif["Feature"] = X_const.columns
vif

Method – 2: Use Principle Component Analysis(PCA)

Step 1: Import Libraries & Create a Dataset with Multicollinearity
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

# Create synthetic dataset with multicollinearity
np.random.seed(42)
X1 = np.random.rand(100) * 100
X2 = X1 + np.random.normal(0, 1, 100)  # Strongly correlated with X1
X3 = np.random.rand(100) * 50

# Target variable
y = 5 + 2 * X1 + 3 * X3 + np.random.normal(0, 10, 100)

# Create DataFrame
df = pd.DataFrame({'X1': X1, 'X2': X2, 'X3': X3, 'y': y})
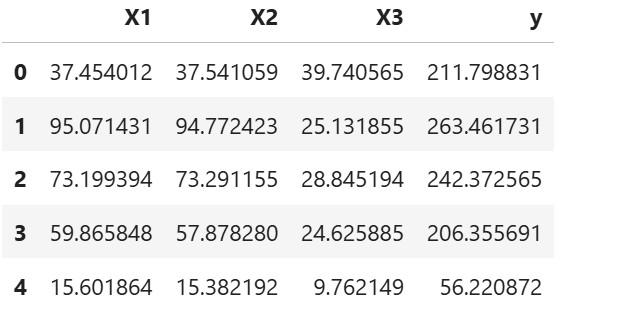
Step 2: Check Correlation Matrix (to confirm multicollinearity)
print(df[['X1', 'X2', 'X3']].corr())
  • You’ll notice that X1 and X2 have correlation close to 1.0 (strong multicollinearity).
Step 3: Standardize the Data
scaler = StandardScaler()
X_scaled = scaler.fit_transform(df[['X1', 'X2', 'X3']])
Step 4: Apply PCA
pca = PCA()
X_pca = pca.fit_transform(X_scaled)

# View explained variance to decide how many components to keep
print(pca.explained_variance_ratio_)
  • You’ll likely see that first 2 components explain >95% of variance.
Step 5: Use Principal Components in Regression
# Keep only first 2 principal components
X_final = X_pca[:, :2]

# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X_final, df['y'], test_size=0.2, random_state=42)

# Fit regression model
model = LinearRegression()
model.fit(X_train, y_train)

# Predict & evaluate
score = model.score(X_test, y_test)
print(f"R² Score (using PCA components): {score:.3f}")
Step 6 : Without Principal Components in Regression
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

# Define features and target
X_original = df[['X1', 'X2', 'X3']]
y = df['y']

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X_original, y, test_size=0.2, random_state=42)

# Train the model
model_original = LinearRegression()
model_original.fit(X_train, y_train)

# Evaluate R² score
r2_original = model_original.score(X_test, y_test)
print(f"R² Score (Before PCA): {r2_original:.3f}")
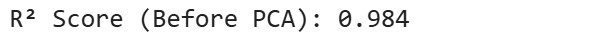
Step 6 : Before And After PCA Comparison

Method – 3: Use Regularization Techniques (Ridge/Lasso)

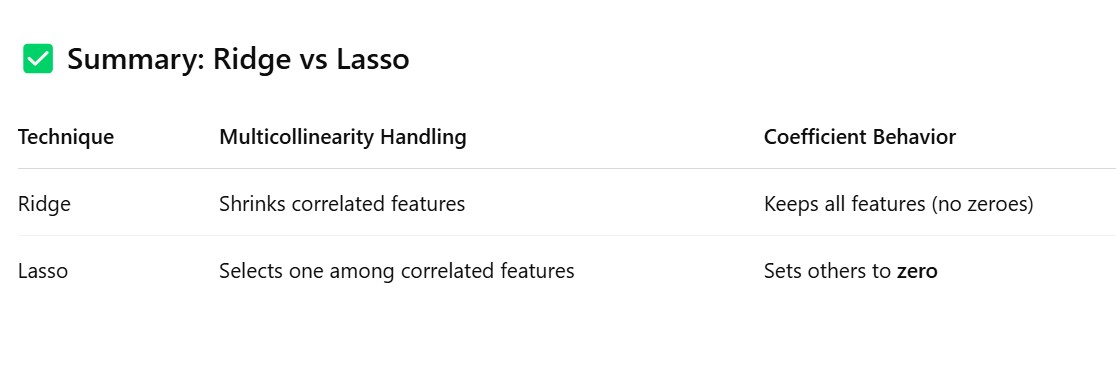
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
import pandas as pd
import numpy as np

# Create synthetic correlated data
np.random.seed(0)
X1 = np.random.rand(100)
X2 = X1 * 0.95 + np.random.rand(100) * 0.05
X3 = X1 * 0.9 + np.random.rand(100) * 0.1
y = 3*X1 + 2*X2 + np.random.rand(100)

X = pd.DataFrame({'X1': X1, 'X2': X2, 'X3': X3})

# Train Ridge model
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
ridge = Ridge(alpha=1.0)
ridge.fit(X_train, y_train)
print("Ridge Coefficients:", ridge.coef_)
print("R² Score:", r2_score(y_test, ridge.predict(X_test)))

Leave a Reply

Your email address will not be published. Required fields are marked *